Numerical methods for indirect approach

The indirect approach to optimal control reformulates the optimal control problem as a system of differential and algebraic equations (DAE) with the values of some variables specified at both ends of the time interval – the two-point boundary value problem (TP–BVP). It is only in special cases that we are able to reformulate the TP–BVP as an initial value problem (IVP), the prominent example of which is the LQR problem and the associate differential Riccati equation solved backwards in time. However, generally we need to solve the TP–BVP DAE and the only way to do it is by numerical methods. Here we give some.

Gradient method for the TP-BVP DAE for free final state

Recall that with the Hamiltonian defined as H(\bm x, \bm u, \bm \lambda) = L(\bm x, \bm u) + \bm \lambda^\top \mathbf f(\bm x, \bm u), the necessary conditions of optimality for the fixed final time and free final state are are given by the following system of differential and algebraic equations (DAE) \begin{aligned} \dot{\bm{x}} &= \nabla_{\bm\lambda} H(\bm x,\bm u,\bm \lambda) \\ \dot{\bm{\lambda}} &= -\nabla_{\bm x} H(\bm x,\bm u,\bm \lambda) \\ \mathbf 0 &= \nabla_{\bm u} H(\bm x,\bm u,\bm \lambda)\qquad (\text{or} \qquad \bm u^\star = \text{argmax } H(\bm x^\star,\bm u, \bm\lambda^\star),\quad \bm u \in\mathcal{U})\\ \bm x(t_\mathrm{i}) &=\mathbf x_\mathrm{i}\\ \bm \lambda(t_\mathrm{f}) &= \nabla\phi(\bm{x}(t_\mathrm{f})). \end{aligned}

One idea to solve this is to guess at the trajectory \bm u(t) on a grid of the time interval, use it to solve the state and costate equations, and then with all the three variables \bm x, \bm u, and \bm u evaluate how much the stationarity equation is actually not satisfied. Based on the this, modify \bm u and go for another iteration. Formally this is expressed as the algorithm:

1. Set some initial trajectory \bm u(t),\; t\in[t_\mathrm{i},t_\mathrm{f}] on a grid of points in [t_\mathrm{i},t_\mathrm{f}].
2. With the chosen \bm u(\cdot) and the initial state \bm x(t_\mathrm{i}), solve the state equation \dot{\bm{x}} = \nabla_{\bm\lambda} H(\bm x,\bm u,\bm \lambda) = \mathbf f(\bm x, \bm u) for \bm x(t) using a solver for initial value problem ODE, that is, on a grid of t\in[t_\mathrm{i},t_\mathrm{f}].
3. Having the control and state trajectories, \bm u(\cdot) and \bm x(\cdot), solve the costate equation \dot{\bm{\lambda}} = -\nabla_{\bm x} H(\bm x,\bm u,\bm \lambda)
   for the costates \bm \lambda(t), starting at the final time t_\mathrm{f}, invoking the boundary condition \bm \lambda(t_\mathrm{f}) = \nabla\phi(\bm{x}(t_\mathrm{f})).
4. Evaluate \nabla_{\bm u} H(\bm x,\bm u,\bm \lambda) for all t\in[t_\mathrm{i}, t_\mathrm{f}].
5. If \nabla_{\bm u} H(\bm x,\bm u,\bm \lambda) \approx \mathbf 0 for all t\in[t_\mathrm{i}, t_\mathrm{f}], quit, otherwise modify \bm u(\cdot) and go to the step 2.

The question is, of course, how to modify \bm u(t) for all t \in [t_\mathrm{i}, t_\mathrm{f}] in the step 4. Recall that the variation of the (augmented) cost functional is \begin{aligned} \delta J^\text{aug} &= [\nabla \phi(\bm x(t_\mathrm{f})) - \bm\lambda(t_\mathrm{f})]^\top \delta \bm{x}(t_\mathrm{f})\\ & \qquad + \int_{t_\mathrm{i}}^{t_\mathrm{f}} [\dot{\bm{\lambda}} +\nabla_{\bm x} H(\bm x,\bm u,\bm \lambda)]^\top \delta \bm x(t)\mathrm{d}t + \int_{t_\mathrm{i}}^{t_\mathrm{f}} [\dot{\bm{x}} - \nabla_{\bm\lambda} H(\bm x,\bm u,\bm \lambda)]^\top \delta \bm\lambda(t) \mathrm{d}t\\ & \qquad + \int_{t_\mathrm{i}}^{t_\mathrm{f}} [\nabla_{\bm u} H(\bm x,\bm u,\bm \lambda)]^\top \delta \bm u(t) \mathrm{d}t \end{aligned}, and for state and costate variables satisfying the state and costate equations this variation simplifies to \delta J^\text{aug} = \int_{t_\mathrm{i}}^{t_\mathrm{f}} [\nabla_{\bm u} H(\bm x,\bm u,\bm \lambda)]^\top \delta \bm u(t) \mathrm{d}t.

Since our goal is to minimize J^\text{aug}, we need to make \Delta J^\text{aug}\leq0. Provided the increment \delta \mathbf u(t)=\bm u^{(i+1)}(t)-\bm u^{(i)}(t) is small, we can consider the linear approximation \delta J^\text{aug} instead. We choose \delta \bm u(t) = -\alpha \nabla_{\bm u} H(\bm x,\bm u,\bm \lambda) for \alpha>0, which means that the control trajectory in the next iteration is \boxed {\bm u^{(i+1)}(t) = \bm u^{(i)}(t) -\alpha \nabla_{\bm u} H(\bm x,\bm u,\bm \lambda),} and the variation of the augmented cost funtion is
\delta J^\text{aug} = -\alpha\int_{t_\mathrm{i}}^{t_\mathrm{f}} [\nabla_{\bm u} H(\bm x,\bm u,\bm \lambda)]^2 \mathrm{d}t \leq 0, and it is zero only for \nabla_{\bm u} H(t,\bm x,\bm u,\bm \lambda) = \mathbf 0 for all t\in[t_\mathrm{i}, t_\mathrm{f}].

Methods for solving TP-BVP ODE

Here we assume that from the stationarity equation \mathbf 0 = \nabla_{\bm u} H(\bm x,\bm u,\bm \lambda) we can express \bm u(t) as a function of the the state and costate variables, \bm x(t) and \bm \lambda(t), respectively. In fact, Pontryagin’s principles gives this expression as \bm u^\star(t) = \text{arg} \min_{\bm u(t) \in\mathcal{U}} H(\bm x^\star(t),\bm u(t), \bm\lambda^\star(t)). And we substitute for \bm u(t) into the state and costate equations. This way we eliminate \bm u(t) from the system of DAEs and we are left with a system of ODEs for \bm x(t) and \bm \lambda(t) only. Formally, the resulting Hamiltonian is a different function as it is now a functio of two variables only.

\begin{aligned} \dot{\bm{x}} &= \nabla_{\bm\lambda} \mathcal H(\bm x,\bm \lambda) \\ \dot{\bm{\lambda}} &= -\nabla_{\bm x} \mathcal H(\bm x,\bm \lambda) \\ \bm x(t_\mathrm{i}) &=\mathbf x_\mathrm{i}\\ \bm x(t_\mathrm{f}) &= \mathbf x_\mathrm{f} \qquad \text{or} \qquad \bm \lambda(t_\mathrm{f}) = \nabla\phi(\bm{x}(t_\mathrm{f})). \end{aligned}

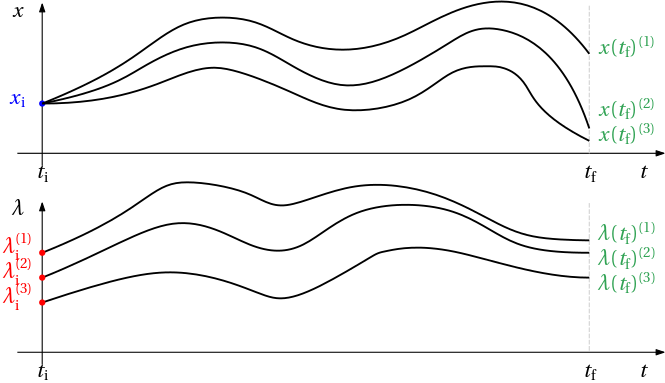
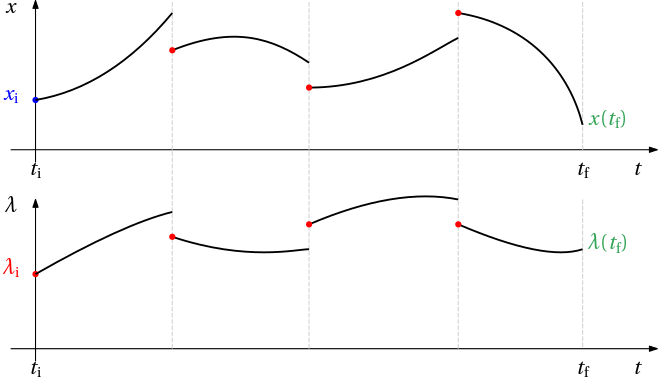
Although we now have an ODE system, it is still a BVP. Strictly speaking, from now on, arbitrary reference on numerical solution of boundary value problems can be consulted to get some overview – we no longer need to restrict ourselves to the optimal control literature and software. On the other hand, the right sides are not quite arbitrary – these are Hamiltonian equations – and this property could and perhaps even should be exploited by the solution methods.

The methods for solving general BVPs are generally divided into

• shooting and multiple shooting methods,
• discretization methods,
• collocation methods.

Shooting methods

Shooting method outside optimal control

Having made the diclaimer that boundary value problems constitute a topic indenendent of the optimal control theory, we start their investigation within a control-unrelated setup. We consider a system of two ordinary differential equations in two variables with the value of the first variable specified at both ends while the value of the other variable is left unspecified \begin{aligned} \begin{bmatrix} \dot y_1(t)\\ \dot y_2(t) \end{bmatrix} &= \begin{bmatrix} f_1(\bm y,t)\\ f_2(\bm y,t) \end{bmatrix}\\ y_1(t_\mathrm{i}) &= \mathrm y_{1\mathrm{i}},\\ y_1(t_\mathrm{f}) &= \mathrm y_{1\mathrm{f}}. \end{aligned}

An idea for a solution method is this:

1. Guess at the missing (unspecified) value y_{2\mathrm{i}} of y_2 at the initial time t_\mathrm{i},
2. Use an IVP solver (for example ode45 in Matlab) to find the values of both variables over the whole interval [t_\mathrm{i},t_\mathrm{f}].
3. Compare the simulated value of the state variable y_1 at the final time t_\mathrm{f} and compare it with the boundary value .
4. Based on the error e = y_1(t_\mathrm{f})-\mathrm y_{1\mathrm{f}}, update y_{2\mathrm{i}} and go back to step 2.

How shall the update in the step 4 be realized? The value of y_1 at the final time t_\mathrm{f} and therefore the error e are functions of the value y_{2\mathrm{i}} of y_2 at the initial time t_\mathrm{i}. We can formally express this upon introducing a map F such that e = F(y_{2\mathrm{i}}). The problem now boils down to solving the nonlinear equation \boxed {F(y_{2\mathrm{i}}) = 0.}

If Newton’s method is to be used for solving this equation, the derivative of F is needed. Most often than not, numerical solvers for IVP ODE have to be called in order to evaluate the function F, in which case the derivative cannot be determined analytically. Finite difference (FD) and algorithmic/automatic differentiation (AD) methods are available.

In this example we only considered y_1 and y_2 as scalar variables, but in general these could be vector variables, in which case a system of equations in the vector variable has to be solved. Instead of a single scalar derivative, its matrix version – Jacobian matrix – must be determined.

By now the reason for calling this method shooting is perhaps obvious. Indeed, the analogy with aiming and shooting a cannon is illustrative.

As another example, we consider the BVP for a pendulum.

Example 1 (BVP for pendulum) For an ideal pendulum described by the second-order model \ddot \theta + \frac{b}{ml^2}\dot \theta + \frac{g}{l} \sin(\theta) = 0 and for a final time t_\mathrm{f}, at which some prescribed value of \theta(t_\mathrm{f}) must be achieved, compute by the shooting method the needed value of the initial angle \theta_\mathrm{i}, while assuming the initial angular rate \omega_\mathrm{i} is zero.

using DifferentialEquations
using Roots
using Plots

function demo_shoot_pendulum()
    θfinal = -0.2;
    tfinal = 3.5;
    tspan = (0.0,tfinal)
    tol = 1e-5
    function pendulum!(dx,x,p,t)
        g = 9.81
        l = 1.0;
        m = 1.0;
        b = 0.1;
        a₁ = g/l
        a₂ = b/(m*l^2)
        θ,ω = x
        dx[1] = ω
        dx[2] = -a₁*sin(θ) - a₂*ω
    end
    prob = ODEProblem(pendulum!,zeros(Float64,2),tspan)
    function F(θ₀::Float64)
        xinitial = [θ₀,0.0]
        prob = remake(prob,u0=xinitial)
        sol = solve(prob,Tsit5(),reltol=tol/10,abstol=tol/10)
        return θfinal-sol[end][1]
    end
    θinitial = find_zero(F,(-pi,pi))    # Solving the equation F(θ)=0 using Roots package. In general can find more solutions.
    xinitial = [θinitial,0.0]
    prob = remake(prob,u0=xinitial)     # Already solved in F(), but we solve it again for plotting.
    sol = solve(prob,Tsit5())
    p1 = plot(sol,lw=2,xlabel="Time",ylabel="Angle",label="θ",idxs=(1))
    scatter!([tfinal],[θfinal],label="Required terminal θ")
    p2 = plot(sol,lw=2,xlabel="Time",ylabel="Angular rate",label="ω",idxs=(2))
    display(plot(p1,p2,layout=(2,1)))
end

demo_shoot_pendulum()

Figure 1: State responses for a pendulum on a given time interval, with zero initial angular rate and the initial angle solved for numerically so that the final angle attains a give value

A few general comments to the above code:

• The function F(\theta_\mathrm{i}) that defines the nonlinear equation F(\theta_\mathrm{i})=0 calles a numerical solver for an IVP ODE. The latter solver then should have the numerical tolerances set more stringent than the former.
• The ODE problem should only be defined once and then in each iteration its parameters should be updated. In Julia, this is done by the remake function, but it may be similar for other languages.

Shooting method for indirect approach to optimal control

We finally bring the method into the realm of indirect approach to optimal control – it is the initial value \lambda_\mathrm{i} of the costate variable that serves as an optimization variable, while the initial value x_\mathrm{i} of the state variable is known and fixed. The final values of both the state and costate variables are the outcomes of numerical simulation obtained using a numerical solver for an IVP ODE. Based on these, the residual is computed. Either as e = x(t_\mathrm{f})-x_\mathrm{f} if the final state is fixed, or as e = \lambda(t_\mathrm{f}) - \nabla \phi(x(t_\mathrm{f})) if the final state is free. Based on this residual, the initial value of the costate is updated and another iteration of the algorithm is entered.

Figure 2: Indirect shooting

Example 2 (Shooting for indirect approach to LQR) Standard LQR optimal control for a second-order system on a fixed finite interval with a fixed final state.

using LinearAlgebra
using DifferentialEquations
using NLsolve

function shoot_lq_fixed(A,B,Q,R,xinitial,xfinal,tfinal)
    n = size(A)[1]
    function statecostateeq!(dw,w,p,t)
        x = w[1:n]
        λ = w[(n+1):end]
        dw[1:n] = A*x - B*(R\B'*λ)
        dw[(n+1):end] = -Q*x - A'*λ
    end
    λinitial = zeros(n)
    tspan = (0.0,tfinal)
    tol = 1e-5
    function F(λinitial)
        winitial = vcat(xinitial,λinitial)
        prob = ODEProblem(statecostateeq!,winitial,tspan)
        dsol = solve(prob,Tsit5(),abstol=tol/10,reltol=tol/10)
        xfinalsolved = dsol[end][1:n]
        return (xfinal-xfinalsolved)
    end
    nsol = nlsolve(F,λinitial,xtol=tol)                 # Could add autodiff=:forward.
    λinitial = nsol.zero                                # Solving once again for plotting.
    winitial = vcat(xinitial,λinitial)
    prob = ODEProblem(statecostateeq!,winitial,tspan)
    dsol = solve(prob,Tsit5(),abstol=tol/10,reltol=tol/10)
    return dsol
end

function demo_shoot_lq_fixed()
    n = 2                                               # Order of the system.
    m = 1                                               # Number of inputs.
    A = rand(n,n)                                       # Matrices modeling the system.
    B = rand(n,m)
        
    Q = diagm(0=>rand(n))                               # Weighting matrices for the quadratic cost function.
    R = rand(1,1)

    xinitial = [1.0, 2.0]
    xfinal = [3.0, 4.0]
    tfinal = 5.0 

    dsol = shoot_lq_fixed(A,B,Q,R,xinitial,xfinal,tfinal)

    p1 = plot(dsol,idxs=(1:2),lw=2,legend=false,xlabel="Time",ylabel="State")
    p2 = plot(dsol,idxs=(3:4),lw=2,legend=false,xlabel="Time",ylabel="Costate")
    display(plot(p1,p2,layout=(2,1)))
end

demo_shoot_lq_fixed()

Figure 3: Shooting method applied to the indirect approach to LQR problem

Multiple shooting methods

The key deficiency of the shooting method is that the only source of the error is the error in the initial condition, this error then amplifies as it propagates over the whole time interval as the numerical integration proceeds, and consequently the residual is very sensitive to tiny changes in the initial value. The multiple shooting method is a remedy for this. The idea is to divide the interval [t_\mathrm{i},t_\mathrm{f}] into N subintervals [t_k,t_{k+1}] and to introduce the values of the state and co-state variable at the beginning of each subinterval as additional variables. Additional equations are then introduced that enforce the continuity of the variable at the end of one subinterval and at the beginning of the next subinterval.

Figure 4: Indirect multiple shooting

Discretization methods

Shooting methods take advantage of availability of solvers for IVP ODEs. These solvers produce discret(ized) trajectories, proceeding (integration) step by step, forward in time. But they do this in a way hidden from users. We just have to set the initial conditions (possibly through numerical optimization) and the solver does the rest.

Alternatively, the formulas for the discrete-time updates are not evaluated one by one, step by step, running forward in time, but are assembled to form a system of equations, in general nolinear ones. Appropriate boundary conditions are then added to these nonlinear equations and the whole system is then solved numerically, yielding a discrete approximation of the trajectories satisfying the BVP.

Since all those equatins are solved simultaneously (as a system of equations), there is no advantage in using explicit methods for solving ODEs, and implicit methods are used instead.

It is now time to recall some crucial results from the numerical methods for solving ODEs. First, we start with the popular single-step methods known as the Runge-Kutta (RK) methods.

We consider the standard ODE \dot x(t) = f(x(t),t).

and we define the Butcher tableau as \begin{array}{ l | c c c c } c_1 & a_{11} & a_{12} & \ldots & a_{1s}\\ c_2 & a_{21} & a_{22} & \ldots & a_{2s}\\ \vdots & \vdots\\ c_s & a_{s1} & a_{s2} & \ldots & a_{ss}\\ \hline & b_{1} & b_{2} & \ldots & b_{s} \end{array}. such that c_i = \sum_{j=1}^s a_{ij}, and 1 = \sum_{j=1}^s b_{j}.

Reffering to the particular Butcher table, a single step of the method is \begin{aligned} f_{k1} &= f(x_k + h_k \left(a_{11}f_{k1}+a_{12}f_{k2} + \ldots + a_{1s}f_{ks}),t_k+c_1h_k\right)\\ f_{k2} &= f(x_k + h_k \left(a_{21}f_{k1}+a_{22}f_{k2} + \ldots + a_{2s}f_{ks}),t_k+c_2h_k\right)\\ \vdots\\ f_{ks} &= f(x_k + h_k \left(a_{s1}f_{k1}+a_{s2}f_{k2} + \ldots + a_{ss}f_{ks}),t_k+c_sh_k\right)\\ x_{k+1} &= x_k + h_k \left(b_1 f_{k1}+b_2f_{k2} + \ldots + b_sf_{ks}\right). \end{aligned}

If the matrix A is strictly lower triangular, that is, if a_{ij} = 0 for all i<j , the method belongs to explicit Runge-Kutta methods, otherwise it belongs to implicit Runge-Kutta methods.

A prominent example of explicit RK methods is the 4-stage RK method (oftentimes referred to as RK4).

Explicit RK4 method

The Buttcher table for the method is \begin{array}{ l | c c c c } 0 & 0 & 0 & 0 & 0\\ 1/2 & 1/2 & 0 & 0 & 0\\ 1/2 & 0 & 1/2 & 0 & 0\\ 1 & 0 & 0 & 1 & 0\\ \hline & 1/6 & 1/3 & 1/3 & 1/6 \end{array}.

Following the Butcher table, a single step of this method is \begin{aligned} f_{k1} &= f(x_k,t_k)\\ f_{k2} &= f\left(x_k + \frac{h_k}{2}f_{k1},t_k+\frac{h_k}{2}\right)\\ f_{k3} &= f\left(x_k + \frac{h_k}{2}f_{k2},t_k+\frac{h_k}{2}\right)\\ f_{k4} &= f\left(x_k + h_k f_{k3},t_k+h_k\right)\\ x_{k+1} &= x_k + h_k \left(\frac{1}{6} f_{k1}+\frac{1}{3}f_{k2} + \frac{1}{3}f_{k3} + \frac{1}{6}f_{k4}\right) \end{aligned}.

But as we have just mentions, explicit methods are not particularly useful for solving BVPs. We prefer implicit methods. One of the simplest is the implicit midpoint method.

Implicit midpoint method

The Butcher tableau is \begin{array}{ l | c r } 1/2 & 1/2 \\ \hline & 1 \end{array}

A single step is then \begin{aligned} f_{k1} &= f\left(x_k+\frac{1}{2}f_{k1} h_k, t_k+\frac{1}{2}h_k\right)\\ x_{k+1} &= x_k + h_k f_{k1}. \end{aligned}

But adding to the last equation x_k we get x_{k+1} + x_k = 2x_k + h_k f_{k1}.

Dividing by two we get \frac{1}{2}(x_{k+1} + x_k) = x_k + \frac{1}{2}h_k f_{k1} and then it follows that \boxed{x_{k+1} = x_k + h_k f\left(\frac{1}{2}(x_k+x_{k+1}),t_k+\frac{1}{2}h_k\right).}

The right hand side of the last equation explains the “midpoint” in the name. It can be viewed as a rectangular approximation to the integral in x_{k+1} = x_k + \int_{t_k}^{t_{k+1}} f(x(t),t)\mathrm{d}t as the integral is computed as an area of a rectangle with the height determined by f() evaluated in the middle point.

Although we do not explain the details here, let’s just note that it is the simplest of the collocation methods. In particular it belongs to Gauss (also Gauss-Legandre) methods.

Implicit trapezoidal method

The method can be viewed both as a single-step (RK) method and a multi-step method. When viewed as an RK method, its Butcher table is \begin{array}{ l | c r } 0 & 0 & 0 \\ 1 & 1/2 & 1/2 \\ \hline & 1/2 & 1/2 \\ \end{array} Following the Butcher table, a single step of the method is then \begin{aligned} f_{k1} &= f(x_k,t_k)\\ f_{k2} &= f(x_k + h_k \frac{f_{k1}+f_{k2}}{2},t_k+h_k)\\ x_{k+1} &= x_k + h_k \left(\frac{1}{2} f_{k1}+\frac{1}{2} f_{k2}\right). \end{aligned}

But since the collocation points are identical with the nodes (grid/mesh points), we can relabel to \begin{aligned} f_{k} &= f(x_k,t_k)\\ f_{k+1} &= f(x_{k+1},t_{k+1})\\ x_{k+1} &= x_k + h_k \left(\frac{1}{2} f_{k}+\frac{1}{2} f_{k+1}\right). \end{aligned}

This possibility is a particular advantage of Lobatto and Radau methods, which contain both end points of the interval or just one of them among the collocation points. The two symbols f_k and f_{k+1} are really just shorthands for values of the function f at the beginning and the end of the integration interval, so the first two equations of the triple above are not really equations to be solved but rather definitions. And we can assemble it all into just one equation \boxed{ x_{k+1} = x_k + h_k \frac{f(x_k,t_k)+f(x_{k+1},t_{k+1})}{2}. }

The right hand side of the last equation explains the “trapezoidal” in the name. It can be viewed as a trapezoidal approximation to the integral in x_{k+1} = x_k + \int_{t_k}^{t_{k+1}} f(x(t),t)\mathrm{d}t as the integral is computed as an area of a trapezoid.

When it comes to building a system of equations within transcription methods, we typically move all the terms just on one side to obtain the defect equations x_{k+1} - x_k - h_k \left(\frac{1}{2} f(x_k,t_k)+\frac{1}{2} f(x_{k+1},t_{k+1})\right) = 0.

Hermite-Simpson method

It belongs to the family of Lobatto III methods, namely it is a 3-stage Lobatto IIIA method. Butcher tableau \begin{array}{ l | c c c c } 0 & 0 &0 & 0\\ 1/2 & 5/24 & 1/3 & -1/24\\ 1 & 1/6 & 2/3 & 1/6\\ \hline & 1/6 & 2/3 & 1/6 \end{array}

Hermite-Simpson method can actually come in three forms (this is from Betts (2020)):

Primary form

There are two equations for the given integration interval [t_k,t_{k+1}] x_{k+1} = x_k + h_k \left(\frac{1}{6}f_k + \frac{2}{3}f_{k2} + \frac{1}{6}f_{k+1}\right), x_{k2} = x_k + h_k \left(\frac{5}{24}f_k + \frac{1}{3}f_{k2} - \frac{1}{24}f_{k+1}\right), where the f symbols are just shorthand notations for values of the function at a certain point f_k = f(x_k,u(t_k),t_k), f_{k2} = f(x_{k2},u(t_{k2}),t_{k2}), f_{k+1} = f(x_{k+1},u(t_{k+1}),t_{k+1}), and the off-grid time t_{k2} is given by t_{k2} = t_k + \frac{1}{2}h_k.

The first of the two equations can be recognized as Simpson’s rule for computing a definite integral. Note that while considering the right hand sides as functions of the control inputs, we also correctly express at which time (the collocation time) we consider the value of the control variable.

Being this general allows considering general control inputs and not only piecewise constant control inputs. For example, if we consider piecewise linear control inputs, then u(t_{k2}) = \frac{u_k + u_{k+1}}{2}. But if we stick to the (more common) piecewise constant controls, not surprisingly u(t_{k2}) = u_k. Typically we format the equations as defect equations, that is, with zero on the right hand side \begin{aligned} x_{k+1} - x_k - h_k \left(\frac{1}{6}f_k + \frac{2}{3}f_{k2} + \frac{1}{6}f_{k+1}\right) &= 0,\\ x_{k2} - x_k - h_k \left(\frac{5}{24}f_k + \frac{1}{3}f_{k2} - \frac{1}{24}f_{k+1}\right) &= 0. \end{aligned}

The optimization variables for every integration interval are x_k,u_k,x_{k2}, u_{k2}.

Hermite-Simpson Separated (HSS) method

Alternatively, we can express f_{k2} in the first equation as a function of the remaining terms and then substitute to the second equation. This will transform the second equation such that only the terms indexed with k and k+1 are present. \begin{aligned} x_{k+1} - x_k - h_k \left(\frac{1}{6}f_k + \frac{2}{3}f_{k2} + \frac{1}{6}f_{k+1}\right) &= 0,\\ x_{k2} - \frac{x_k + x_{k+1}}{2} - \frac{h_k}{8} \left(f_k - f_{k+1}\right) &= 0. \end{aligned}

While we already know (from some paragraph above) that the first equation is Simpson’s rule, the second equation is an outcome of Hermite intepolation. Hence the name. The optimization variables for every integration interval are the same as before, that is, x_k,u_k,x_{k2}, u_{k2} .

Hermite-Simpson Condensed (HSC) method

Yet some more simplification can be obtained from HSS. Namely, the second equation can be actually used to directly prescribe x_{k2} x_{k2} = \frac{x_k + x_{k+1}}{2} + \frac{h_k}{8} \left(f_k - f_{k+1}\right), which is used in the first equation as an argument for the f() function (represented by the f_{k2} symbol), by which the second equation and the term x_{k2} are eliminated from the set of defect equations. The optimization variables for every integration interval still need to contain u_{k2} even though x_{k2} was eliminated, because it is needed to parameterize f_{k2} . That is, the optimization variables then are x_k,u_k, u_{k2} . Reportedly (by Betts) this has been widely used and historically one of the first methods. When it comes to using it in optimal control, it turns out, however, that the sparsity pattern is better for the HSS.

Collocation methods

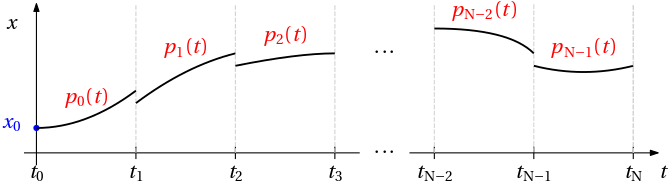
Yet another family of methods for solving BVP ODE \dot x(t) = f(x(t),t) are collocation methods. They are also based on discretization of independent variable – the time t. That is, on the interval [t_\mathrm{i}, t_\mathrm{f}], discretization points (or grid points or nodes or knots) are chosen, say, t_0, t_1, \ldots, t_N, where t_0 = t_\mathrm{i} and t_N = t_\mathrm{f}. The solution x(t) is then approximated by a polynomial p_k(t) of a certain degree s on each interval [t_k,t_{k+1}] of length h_k=t_{k+1}-t_k

p_k(t) = p_{k0} + p_{k1}(t-t_k) + p_{k2}(t-t_k)^2+\ldots + p_{ks}(t-t_k)^s.

The degree of the polynomial is low, say s=3 or so, certainly well below 10. With N subintervals, the total number of coefficients to parameterize the (approximation of the) solution x(t) over the whole interval is then N(s+1). For example, for s=3 and N=10, we have 40 coefficients: p_{00}, p_{01}, p_{02}, p_{03}, p_{10}, p_{11}, p_{12}, p_{13},\ldots, p_{90}, p_{91}, p_{92}, p_{93}.

Figure 5: Indirect collocation

Finding a solution amounts to determining all those coefficients. Once we have them, the (approximate) solution is given by a piecewise polynomial.

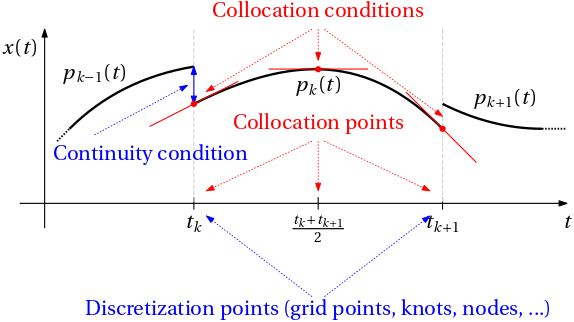
How to determine the coefficients? By interpolation. But we will see in a moment that two types of interpolation are needed – interpolation of the value of the solution and interpolation of the derivative of the solution.

The former is only performed at the beginning of each interval, that is, at every discretization point (or grid point or node or knot). The condition reads that the polynomial p_{k-1}(t) approximating the solution x(t) on the (k-1)th interval should attain the same value at the end of that interval, that is, at t_{k-1} + h_{k-1}, as the polynomial p_k(t) approximating the solution x(t) on the kth interval attains at the same point, which from its perspective is the beginning of the kth interval, that is, t_k. We express this condition formally as \boxed{p_{k-1}(\underbrace{t_{k-1}+h_{k-1}}_{t_{k}}) = p_k(t_k).}

Expanding the two polynomials, we get p_{k-1,0} + p_{k-1,1}h_{k-1} + p_{k-1,2}h_{k-1}^2+\ldots + p_{k-1,s}h_{k-1}^s = p_{k0}.

Subscripts in the coefficients

We adopt the notational convention that a coefficient of a polynomial is indexed by two indices, the first one indicating the interval and the second one indicating the power of the corresponding term. For example, p_{k-1,2} is the coefficient of the quadratic term in the polynomial approximating the solution on the (k-1)th interval. For the sake of brevity, we omit the comma between the two subscripts in the cases such as p_{k1} (instead of writing p_{k,1}). But we do write p_{k-1,0}, because here omiting the comma would introduce ambiguity.

Good, we have one condition (one equation) for each subinterval. But we need more, if polynomials of degree at least one are considered (we then parameterize them by two parameters, in which case one more equation is needed for each subinterval). Here comes the opportunity for the other kind of interpolation – interpolation of the derivative of the solution. At a given point (or points) that we call collocation points, the polynomial p_k(t) approximating the solution x(t) on the kth interval should satisfy the same differential equation \dot x(t) = f(x(t),t) as the solution does. That is, we require that at

t_{kj} = t_k + h_k c_{j}, \quad j=1,\ldots, s, which we call collocation points, the polynomial satisfies \boxed{\dot p_k(t_{kj}) = f(p_k(t_{kj}),t_{kj}), \quad j=1,\ldots, s.}

Expressing the derivative of the polynomial on the left and expanding the polynomial itself on the right, we get \begin{aligned} p_{k1} + &2p_{k2}(t_{kj}-t_k)+\ldots + s p_{ks}(t_{kj}-t_k)^{s-1} = \\ &f(p_{k0} + p_{k1}(t_{kj}-t_k) + p_{ks}(t_{kj}-t_k)^2 + \ldots + p_{ks}(t_{kj}-t_k)^s), \quad j=1,\ldots, s. \end{aligned}

This gives us the complete set of equations for each interval. For the considered example of a cubic polynomial, we have one interpolation condition at the beginning of the interval and then three collocation conditions at the collocation points. In total, we have four equations for each interval. The number of equations is equal to the number of coefficients of the polynomial. Before the system of equations can solved for the coefficients, we must specifies the collocation points. Based on these, the collocation methods split into three families:

• Gauss or Gauss-Legendre methods – the collocation points are strictly inside each interval.
• Lobatto methods – the collocation points include also both ends of each interval.
• Radau methods – the collocation points include just one end of the interval.

Figure 6: Single (sub)interval in indirect collocation – a cubic polynomial calls for three collocation points, two of which coincide with the discretization points (discrete-times); the continuity is enforced at the discretization point at the beginning of the interval

Important

Although in principle the collocation points could be arbitrary (but distinct), within a given family of methods, and for a given number of collocation points, some clever options are known that maximize accuracy.

Linear polynomials

Besides the piecewise constant approximation, which is too crude, not to speak of the discontinuity it introduces, the next simplest approximation of a solution x(t) on the interval [t_k,t_{k+1}] of length h_k=t_{k+1}-t_k is a linear (actually affine) polynomial p_k(t) = p_{k0} + p_{k1}(t-t_k).

On the given kth interval it is parameterized by two parameters p_{k0} and p_{k1}, hence two equations are needed. The first equation enforces the continuity at the beginning of the interval \boxed {p_{k-1,0} + p_{k-1,1}h_{k-1} = p_{k0}.}

The remaining single equation is the collocation condition at a single collocation point t_{k1} = t_k + h_k c_1, which remains to be chosen. One possible choice is c_1 = 1/2, that is t_{k1} = t_k + \frac{h_k}{2}

In words, the collocation point is chosen in the middle of the interval. The collocation condition then reads \boxed {p_{k1} = f\left(p_{k0} + p_{k1}\frac{h_k}{2}\right).}

Quadratic polynomials

If a quadratic polynomial is used to approximate the solution, the condition at the beginning of the interval is \boxed {p_{k-1,0} + p_{k-1,1}h_{k-1} + p_{k-1,2}h_{k-1}^2 = p_{k0}.}

Two more equations – collocation conditions – are needed to specify all the three coefficients that parameterize the aproximating polynomial on a given interval [t_k,t_{k+1}]. One intuitive (and actually clever) choice is to place the collocation points at the beginning and the end of the interval, that is, at t_k and t_{k+1}. The coefficient that parameterize the relative position of the collocation points with respect to the interval are c_1=0 and c_2=1 The collocation conditions then read \boxed {\begin{aligned} p_{k1} &= f(p_{k0}),\\ p_{k1} + 2p_{k2}h_{k} &= f(p_{k0} + p_{k1}h_k + p_{k2}h_k^2). \end{aligned}}

Cubic polynomials

When a cubic polynomial is used, the condition at the beginning of the kth interval is \boxed {p_{k-1,0} + p_{k-1,1}h_{k-1} + p_{k-1,2}h_{k-1}^2+p_{k-1,3}h_{k-1}^3 = p_{k0}.}

Three more equations are needed to determine all the four coefficients of the polynomial. Where to place the collocations points? One intuitive (and clever too) option is to place them at the beginning, in the middle, and at the end of the interval. The relative positions of the collocation points are then given by c_1=0, c_2=1/2, and c_3=1. The collocation conditions then read \boxed {\begin{aligned} p_{k1} &= f\left(p_{k0} + p_{k1}(t_{k1}-t_k) + p_{k2}(t_{k1}-t_k)^2 + p_{k3}(t_{k1}-t_k)^3\right),\\ p_{k1} + 2p_{k2}\frac{h_k}{2} + 3 p_{k3}\left(\frac{h_k}{2}\right)^{2} &= f\left(p_{k0} + p_{k1}\frac{h_k}{2} + p_{k2}\left(\frac{h_k}{2}\right)^2 + p_{k3}\left(\frac{h_k}{2} \right)^3\right),\\ p_{k1} + 2p_{k2}h_k + 3 p_{k3}h_k^{2} &= f\left(p_{k0} + p_{k1}h_k + p_{k2}h_k^2 + p_{k3}h_k^3\right). \end{aligned}}

Collocation methods are implicit Runge-Kutta methods

An important observation that we are goint to make is that collocation methods can be viewed as implicit Runge-Kutta methods. But not all IRK methods can be viewed as collocation methods. In this section we show that the three implicit RK methods that we covered above are indeed (equivalent to) collocation methods. By the equivalence we mean that there is a linear relationship between the coefficients of the polynomials that approximate the solution on a given (sub)interval and the solution at the discretization point together with the derivative of the solution at the collocation points.

Implicit midpoint method as a Radau collocation method

For the given integration interval [t_k,t_{k+1}], we write down two equations that relate the two coefficients of the linear polynomial p_k(t) = p_{k0} + p_{k1}(t-t_k) and an approximation x_k of x(t) at the beginning of the interval t_k, as well as an approximation of \dot x(t) at the (single) collocation point t_{k1} = t_{k} + \frac{h_k}{2}.

In particular, the first interpolation condition is p_k(t_k) = \textcolor{red}{p_{k0} = x_k} \approx x(t_k).

The second interpolation condition, the one on the derivative in the middle of the interval is \dot p_k\left(t_k + \frac{h_k}{2}\right) = \textcolor{red}{p_{k1} = f(x_{k1},t_{k1})} \approx f(x(t_{k1}),t_{k1}).

Note that here we introduced yet another unknown – the approximation x_{k1} of x(t_{k1}) at the collocation point t_{k1}. We can write it using the polynomial p_k(t) as x_{k1} = p_k\left(t_k + \frac{h_k}{2}\right) = p_{k0} + p_{k1}\frac{h_k}{2}.

Substituting for p_{k0} and p_{k1}, we get x_{k1} = x_k + f(x_{k1},t_{k1})\frac{h_k}{2}.

We also introduce the notation f_{k1} for f(x_{k1},t_{k1}) and we can write an equation f_{k1} = f\left(x_k + f_{k1}\frac{h_k}{2}\right).

But we want to find x_{k+1}, which we can accomplish by evaluating the polynomial p_k(t) at t_{k+1} = t_k+h_k x_{k+1} = x_k + f_{k1}h_k.

Collecting the last two equations, we rederived the good old friend – the implicit midpoint method.

Implicit trapezoidal method as a Lobatto collocation method

For the given integration interval [t_k,t_{k+1}], we write down three equations that relate the three coefficients of the quadratic polynomial p_k(t) = p_{k0} + p_{k1}(t-t_k) + p_{k2}(t-t_k)^2 and an approximation x_k of x(t) at the beginning of the interval t_k, as well as approximations to \dot x(t) at the two collocations points t_k and t_{k+1}.

In particular, the first interpolation condition is p_k(t_k) = \textcolor{red}{p_{k0} = x_k} \approx x(t_k).

The second interpolation condition, the one on the derivative at the beginning of the interval, the first collocation point, is \dot p_k(t_k) = \textcolor{red}{p_{k1} = f(x_k,t_k)} \approx f(x(t_k),t_k).

The third interpolation condition, the one on the derivative at the second collocation point \dot p_k(t_k+h_k) = \textcolor{red}{p_{k1} + 2p_{k2} h_k = f(x_{k+1},t_{k+1})} \approx f(x(t_{k+1}),t_{k+1}).

All the three conditions (emphasized in color above) can be written together as \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 1 & 2 h_k\\ \end{bmatrix} \begin{bmatrix} p_{k0} \\ p_{k1} \\ p_{k2} \end{bmatrix} = \begin{bmatrix} x_{k} \\ f(x_k,t_k) \\ f(x_{k+1},t_{k+1}) \end{bmatrix}.

The above system of linear equations can be solved by inverting the matrix \begin{bmatrix} p_{k0} \\ p_{k1} \\ p_{k2} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -\frac{1}{2h_k} & \frac{1}{2h_k}\\ \end{bmatrix} \begin{bmatrix} x_{k} \\ f(x_k,t_k) \\ f(x_{k+1},t_{k+1}) \end{bmatrix}.

We can now write down the interpolating/approximating polynomial p_k(t) = x_{k} + f(x_{k},t_{k})(t-t_k) +\left[-\frac{1}{2h_k}f(x_{k},t_{k}) + \frac{1}{2h_k}f(x_{k+1},t_{k+1})\right](t-t_k)^2.

This polynomial can now be used to find an (approximation of the) value of the solution at the end of the interval x_{k+1} = p_k(t_k+h_k) = x_{k} + f(x_{k},t_{k})h_k +\left[-\frac{1}{2h_k}f(x_{k},t_{k}) + \frac{1}{2h_k}f(x_{k+1},t_{k+1})\right]h_k^2, which can be simplified nearly upon inspection to x_{k+1} = x_{k} + \frac{f(x_{k},t_{k}) + f(x_{k+1},t_{k+1})}{2} h_k, but this is our good old friend, isn’t it? We have shown that the collocation method with a quadratic polynomial with the collocation points chosen at the beginning and the end of the interval is (equivalent to) the implicit trapezoidal method. The method belongs to the family of Lobatto IIIA methods, which are all known to be collocation methods.

Hermite-Simpson method as a Lobatto collocation method

Here we show that Hermite-Simpson method also qualifies as a collocation method. In particular, it belongs to the family of Lobatto IIIA methods, similarly as implicit trapezoidal method. The first condition, the one on the value of the cubic polynomial p_k(t) = p_{k0} + p_{k1}(t-t_k) + p_{k2}(t-t_k)^2+ p_{k3}(t-t_k)^3 at the beginning of the interval is p_k(t_k) = \textcolor{red}{p_{k0} = x_k} \approx x(t_k).

The three remaining conditions are imposed at the collocation points, which for the integration interval [t_k,t_{k+1}] are t_{k1} = t_k , t_{k2} = \frac{t_k+t_{k+1}}{2} , and t_{k3} = t_{k+1}. With the first derivative of the polynomial given by \dot p_k(t) = p_{k1} + 2p_{k2}(t-t_k) + 3p_{k3}(t-t_k)^2, the first collocation condition \dot p_k(t_k) = \textcolor{red}{p_{k1} = f(x_k,t_k)} \approx f(x(t_k),t_k).

The second collocation condition – the one on the derivative in the middle of the interval – is \dot p_k\left(t_k+\frac{1}{2}h_k\right) = \textcolor{red}{p_{k1} + 2p_{k2} \frac{h_k}{2} + 3p_{k3} \left(\frac{h_k}{2}\right)^2 = f(x_{k2},t_{k2})} \approx f\left(x\left(t_{k}+\frac{h_k}{2}\right),t_{k}+\frac{h_k}{2}\right).

The color-emphasized part can be simplified to \textcolor{red}{p_{k1} + p_{k2} h_k + \frac{3}{4}p_{k3} h_k^2 = f(x_{k2},t_{k2})}.

Finally, the third collocation condition – the one imposed at the end of the interval – is \dot p_k(t_k+h_k) = \textcolor{red}{p_{k1} + 2p_{k2} h_k + 3p_{k3} h_k^2 = f(x_{k+1},t_{k+1})} \approx f(x(t_{k+1}),t_{k+1}).

All the four conditions (emphasized in color above) can be written together as \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 1 & h_k & \frac{3}{4} h_k^2\\ 0 & 1 & 2 h_k & 3h_k^2\\ \end{bmatrix} \begin{bmatrix} p_{k0} \\ p_{k1} \\ p_{k2} \\p_{k3} \end{bmatrix} = \begin{bmatrix} x_{k} \\ f(x_k,t_k) \\ f(x_{k2},t_{k2}) \\ f(x_{k+1},t_{k+1}). \end{bmatrix}

Inverting the matrix analytically, we get \begin{bmatrix} p_{k0} \\ p_{k1} \\ p_{k2}\\ p_{k3} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & -\frac{3}{2h_k} & \frac{2}{h_k} & -\frac{1}{2h_k}\\ 0 & \frac{2}{3h_k^2} & -\frac{4}{3h_k^2} & \frac{2}{3h_k^2} \end{bmatrix} \begin{bmatrix} x_{k} \\ f(x_k,t_k) \\ f(x_{k2},t_{k2})\\ f(x_{k+1},t_{k+1}). \end{bmatrix}.

We can now write down the interpolating/approximating polynomial \begin{aligned} p_k(t) &= x_{k} + f(x_{k},t_{k})(t-t_k) +\left[-\frac{3}{2h_k}f(x_{k},t_{k}) + \frac{2}{h_k}f(x_{k2},t_{k2}) -\frac{1}{2h_k}f(x_{k+1},t_{k+1}) \right](t-t_k)^2\\ & +\left[\frac{2}{3h_k^2}f(x_{k},t_{k}) - \frac{4}{3h_k^2}f(x_{k2},t_{k2}) +\frac{2}{3h_k^2}f(x_{k+1},t_{k+1}) \right](t-t_k)^3. \end{aligned}

We can use this prescription of the polynomial p_k(t) to compute the (approximation of the) value of the solution at the end of the kth interval \begin{aligned} x_{k+1} = p_k(t_k+h_k) &= x_{k} + f(x_{k},t_{k})h_k +\left[-\frac{3}{2h_k}f(x_{k},t_{k}) + \frac{2}{h_k}f(x_{k2},t_{k2}) -\frac{1}{2h_k}f(x_{k+1},t_{k+1}) \right]h_k^2\\ & +\left[\frac{2}{3h_k^2}f(x_{k},t_{k}) - \frac{4}{3h_k^2}f(x_{k2},t_{k2}) +\frac{2}{3h_k^2}f(x_{k+1},t_{k+1}) \right]h_k^3, \end{aligned} which can be simplified to \begin{aligned} x_{k+1} &= x_{k} + f(x_{k},t_{k})h_k +\left[-\frac{3}{2}f(x_{k},t_{k}) + \frac{2}{1}f(x_{k2},t_{k2}) -\frac{1}{2}f(x_{k+1},t_{k+1}) \right]h_k\\ & +\left[\frac{2}{3}f(x_{k},t_{k}) - \frac{4}{3}f(x_{k2},t_{k2}) +\frac{2}{3}f(x_{k+1},t_{k+1}) \right]h_k, \end{aligned} which further simplifies to x_{k+1} = x_{k} + h_k\left[\frac{1}{6}f(x_{k},t_{k}) + \frac{2}{3}f(x_{k2},t_{k2}) + \frac{1}{6}f(x_{k+1},t_{k+1}) \right], which can be recognized as the Simpson integration that we have already seen in implicit Runge-Kutta method described above.

Obviously f_{k2} needs to be further elaborated on, namely, x_{k2} needs some prescription too. We know that it was introduced as an approximation to the solution x in the middle of the interval. Since the value of the polynomial in the middle is such an approximation too, we can set x_{k2} equal to the value of the polynomial in the middle. \begin{aligned} x_{k2} = p_k\left(t_k+\frac{1}{2}h_k\right) &= x_{k} + f(x_{k},t_{k})\frac{h_k}{2} +\left[-\frac{3}{2h_k}f(x_{k},t_{k}) + \frac{2}{h_k}f(x_{k2},t_{k2}) -\frac{1}{2h_k}f(x_{k+1},t_{k+1}) \right]\left(\frac{h_k}{2}\right)^2\\ & +\left[\frac{2}{3h_k^2}f(x_{k},t_{k}) - \frac{4}{3h_k^2}f(x_{k2},t_{k2}) +\frac{2}{3h_k^2}f(x_{k+1},t_{k+1}) \right]\left(\frac{h_k}{2}\right)^3, \end{aligned} which without further ado simplifies to x_{k2} = x_{k} + h_k\left( \frac{5}{24}f(x_{k},t_{k}) +\frac{1}{3}f(x_{k2},t_{k2}) -\frac{1}{24}f(x_{k+1},t_{k+1}) \right), which can be recognized as the other equation in the primary formulation of Implicit trapezoidal method described above.

Pseudospectral collocation methods

They only consider a single polynomial over the whole interval. The degree of such polynomial, in contrast with classical collocation methods, rather high, therefore also the number of collocation points is high, but their location is crucial.

References

Betts, John T. 2020. Practical Methods for Optimal Control Using Nonlinear Programming. 3rd ed. Advances in Design and Control. Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9781611976199.