Numerical methods for direct approach

We have already seen that direct methods for discrete-time optimal control problems essentially just regroup and reshape the problem data so that a nonlinear programming (NLP) solver can accept them. In order to follow the same approach with continuous-time optimal control problems, some kind of discretization is inevitable in order to formulate a nonlinear program. Depending of what is discretized and how, several groups of methods can be identified

The core principles behind the methods are identical to those discussed in the previous section on numerical methods for indirect approaches, but the adjective “direct” suggests that there must be some modifications.

Direct shooting methods

In contrast with the application of shooting methods to the TP-BVP originating from the indirect approach, here the variables through whose values we aim the fictitious cannon are not the initial co-state vector but the (possibly long) vector parameterizing the whole control trajectory.

In the simplest – and fairly practical – case of a piecewise constant control trajectory, which is motivated by the eventual discrete-time implementation using a zero-order hold (ZOH), the control trajectory is parameterized just by the sequence of values u_0, u_1, \ldots, u_{N-1}.

Figure 1: Direct shooting – only the control trajectory is discretized and the parameters of this discretization serve as optimization variables

The state trajectory x(t) corresponding to the fixed initial state \mathrm x_\mathrm{i} and the sequence of controls is obtained by using some IVP ODE numerical solver.

For the chosen control trajectory and the simulated state trajectory, the cost function J(u(\cdot);x_\mathrm{i}) = \phi(x(t_\mathrm{f}),t_\mathrm{f}) + \int L(x,u) \mathrm d t is then evaluated. This can also only be done numerically, typically using methods for numerical integration.

Once the cost function is evaluated, numerical optimization solver is used to update the vector parameterizing the control trajectory so that the cost is reduced. For the new control trajectory, the state response is simulated, … and so on.

Since optimization is only done over the optimization variables that parameterize the control trajectory, the method resembles the sequential method of the direct approach to discrete-time optimal control.

Direct multiple shooting methods

…

Direct transcription methods

In contrast with the direct shooting methods, here both the control and state trajectories are discretized. There is then no need for a numerical solver for IVP ODE.

Figure 2: Direct transcription/discretization – both the control and state trajectories are discretized and the resulting vectors of parameterers of this discretization serve as optimization variables

The optimization is then done over the optimization variables that parameterize both the control trajectory and the state trajectory. In this regard the methods resemble the simultaneous method of the direct approach to discrete-time optimal control.

Direct collocation methods

Similarly as in the direct transcription methods, both the control and state trajectories are discretized and the parameterization of this discretization enters the optimization.

But here it is not just the values of the state and the control variables at the discretization points that are the optimization variables, but rather the coefficients of the polynomials that approximate the corresponding variables at the intermediate times between the discretization points.

Figure 3: Direct collocation – both the control and state trajectories are approximated by piecewise polynomials and parameters of these polynomials serve as optimization variables

However, similarly as we have already seen while discussing the collocation methods for the indirect approach, every direct collocation methods is equivalent to some direct transcription method. For example, collocation with a quadratic polynomial and the collocation points at the beginning and end of the interval is equivalent to the implicit trapezoidal rule. Some people even say that the implicit trapezoidal method is a collocation method.

Minimum‐time optimal control in direct approach

While the indirect approach to optimal control allows for relaxing the final time t_\mathrm{f} (and possibly including it in the cost function), the direct approach does not seem to support it. The final time has to be finite and constant.

Here we show one way to turn the final time is t_\mathrm{f} into an optimization variable. We achieve it by augmenting the state equations with a new variable… guess what… t_\mathrm{f} accompanied with the corresponding state equation \dot t_\mathrm{f} = 0.

We now introduce a new normalized time variable \tau\in [0,1] such that t = \tau t_\mathrm{f}.

The differentials of time then relate correspondingly \mathrm{d} t = t_\mathrm{f}\mathrm{d}\tau.

The original state equation \frac{\mathrm{d}x}{\mathrm{d}t} = f(x) then modifies to \boxed{ \frac{\mathrm{d}x}{\mathrm{d}\tau} = t_\mathrm{f} f(x).}

Strictly speaking this should be \frac{\mathrm{d}\hat x}{\mathrm{d}\tau} = t_\mathrm{f} f(\hat x), reflecting that x(t) = x(t_\mathrm{r} \tau) = \hat x(\tau) . But the abuse of notation is perhaps acceptable.

The cost function will then include a term penalizing t_\mathrm{f}. Or perhaps the whole cost function is just t_\mathrm{f} .Or perhaps the final time does not even have to be penalized at all, it is just an optimization variable, it just adds a degree of freedom to the optimal control problem. Of course, in the latter case this is no longer a minimum-time problem, just a free-final time problem.

In direct transcription methods for optimal control, the number of discretization/integration (sub)intervals is fixed and not subject to optimization, otherwise the resulting NLP would have a varying size for a varying final time, which is not convenient. Instead, the length of the integration interval, or the discretization/sampling interval is varied hN = t_\mathrm{f}.

Recall that all (single-step) discretization methods can be interpreted as an approximate computation of the definite integral in x_{k+1} = x_k + \int_{t_k}^{t_{k+1}} f(x(t),t)\mathrm{d}t, which in s-stage Runge-Kutta methods with a fixed time step h always looks like x_{k+1} = x_k + h \sum_{j=1}^s b_{j} f_{kj}.

Since the length of the integration interval h is now an optimization variable, even a problem that is originally linear is now turned into a nonlinear one. Furthermore, we can see consistency between x_{k+1} = x_k + \frac{t_\mathrm{f}}{N} \sum_{j=1}^s b_{j} f_{kj} and the above result for the continuous-time problem that does not consider discretization.

Example 1 (Time-optimal river crossing) Sinusoidal bank shape, bell-shape river current, controlling only the orientation of the boat, but with some dynamics too.

Show the code 
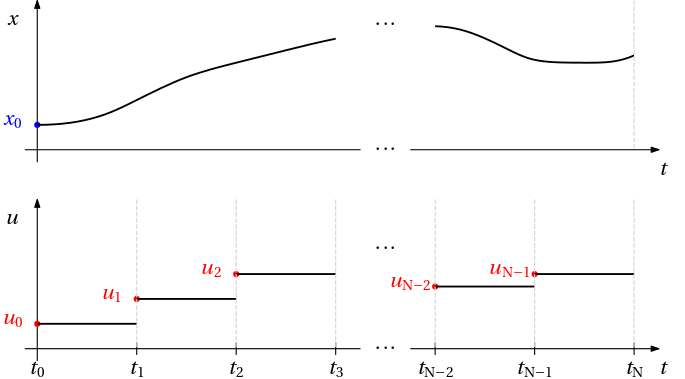
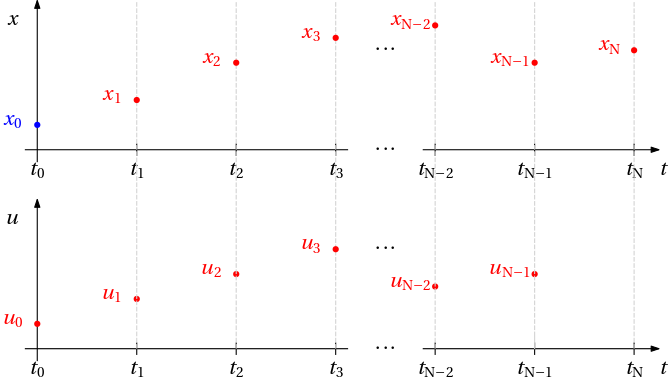
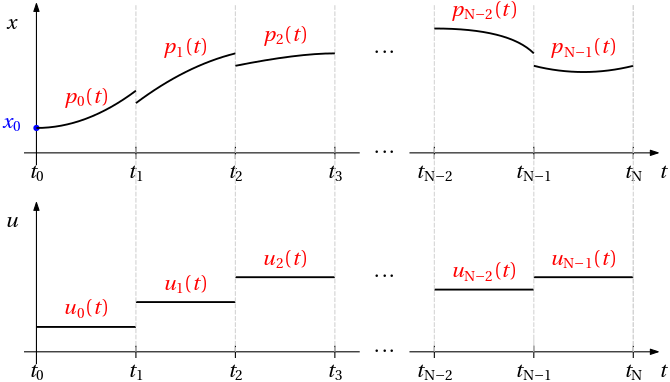
using Plots
using JuMP
using Ipopt
using Interpolations

function river_crossing_direct_transcription()
    wmax = 1.0                                          # One half of the width of the river.
    Rmax = 3.0                                          # Can set opposite direction of flow with MINUS sign.
    R(w) = Rmax*exp(-(w/wmax)^2)                        # Velocity of the river as a function of the distance from the center.
    u(x,y) = R(y-sin(x))/sqrt(1+cos(x)^2)               # x-component of the velocity of the flow.
    v(x,y) = R(y-sin(x))*cos(x)/sqrt(1+cos(x)^2)        # y-component of the velocity of the flow.
    Vmax = 4.0                                          # Maximum velocity of the boat with respect to the mass of water.
    V̇max = 100.0
    θ̇max = 5
    (xinitial,yinitial) = (0.0,-wmax)                   # Initial position of the boat.
    (xfinal,yfinal) = (2*pi,wmax)                       # Final required position of the boat.
    tfinal_0 = 5.0                                      # Initial guess for the final time.
    N = 50                                              # Number of time steps.
    f₁(x,y,V,θ) = V*cos(θ) + u(x,y)                     # Dynamics of the boat.
    f₂(x,y,V,θ) = V*sin(θ) + v(x,y)
    model = Model(Ipopt.Optimizer)
    set_silent(model)
    @variable(model,tfinal>=0,start=tfinal_0)           # Final time as an optimization variable.
    h = tfinal/N                                        # Time step.
    @variable(model, x[1:N+1])                          # N+1 values, because needed at the initial and final times.
    @variable(model, y[1:N+1])                          # N+1 values, because needed at the initial and final conditions.
    @variable(model, 0.0 <= V[1:N] <= Vmax)             # N values, because not needed at the final one.
    @variable(model, θ[1:N])                            # N values, because not needed at the final one.
    for i in 1:(N-1)
        @constraint(model, x[i+1] == x[i] + h*(f₁(x[i],y[i],V[i],θ[i])+f₁(x[i+1],y[i+1],V[i+1],θ[i+1]))/2)
        @constraint(model, y[i+1] == y[i] + h*(f₂(x[i],y[i],V[i],θ[i])+f₂(x[i+1],y[i+1],V[i+1],θ[i+1]))/2)
    end
    @constraint(model, x[N+1] == x[N] + h*(f₁(x[N],y[N],V[N],θ[N])+f₁(x[N+1],y[N+1],V[N],θ[N]))/2)  # Over the last integration interval.
    @constraint(model, y[N+1] == y[N] + h*(f₂(x[N],y[N],V[N],θ[N])+f₂(x[N+1],y[N+1],V[N],θ[N]))/2)
    @expression(model, southern_bank[i=1:N+1],sin(x[i])-wmax)
    @expression(model, northern_bank[i=1:N+1],sin(x[i])+wmax)
    @constraint(model, [i=1:N+1], southern_bank[i] <= y[i])                 # Constraints on the y coordinate.
    @constraint(model, [i=1:N+1], northern_bank[i] >= y[i])                 # Constraints on the y coordinate. 
    @constraint(model, [i=1:N-1], -V̇max*h <= V[i+1]-V[i])                   # Constraints on the rate of change of the forward velocity.
    @constraint(model, [i=1:N-1], V̇max*h >= V[i+1]-V[i])                    # Constraints on the rate of change of the forward velocity.
    @constraint(model, [i=1:N-1], -θ̇max*h <= θ[i+1]-θ[i])                   # Constraints on the rate of change of the angular velocity.
    @constraint(model, [i=1:N-1], θ̇max*h >= θ[i+1]-θ[i])                    # Constraints on the rate of change of the angular velocity.
    interp_linear_x = linear_interpolation([1, N+1], [xinitial, xfinal])    # Linear growth.
    interp_linear_y = linear_interpolation([1, N+1], [yinitial, yfinal])    # Linear growth.
    interp_linear_θ = linear_interpolation([1, N÷2, N], [1.0, 0.0, 1.0])    # V profile.
    initial_guess_x = mapreduce(transpose, vcat, interp_linear_x.(1:N+1))   # Converting a vector of vectors to a matrix.
    initial_guess_y = mapreduce(transpose, vcat, interp_linear_y.(1:N+1))
    initial_guess_V = Vmax*ones(N)                                          # Initial guess for the forward velocity: just max.
    # initial_guess_θ = zero(initial_guess_V)
    initial_guess_θ = mapreduce(transpose, vcat, interp_linear_θ.(1:N))
    set_start_value.(x, initial_guess_x)
    set_start_value.(y, initial_guess_y)
    set_start_value.(V, initial_guess_V)
    set_start_value.(θ, initial_guess_θ)
    fix(x[1], xinitial)                                                     # Setting the initial positions.
    fix(y[1], yinitial)
    fix(x[N+1], xfinal)                                                     # Setting the final positions.
    fix(y[N+1], yfinal) 
    @objective(model, Min, tfinal)                                          # Cośt function for the minimum-time control.
    optimize!(model)
    println("""
    termination_status = $(termination_status(model))
    primal_status      = $(primal_status(model))
    objective_value    = $(objective_value(model))
    """)
    gr(lw=2,label="",ls=:solid,markershape=:circle)
    t = value(h)*(0:N)
    p1 = plot(t[1:end-1],value.(V),ylabel="V",xlabel="t",seriestype=:steppost,ylims=(-0.1,1.1*Vmax))
    p2 = plot(t[1:end-1],value.(θ),ylabel="θ",xlabel="t",seriestype=:steppost)
    pA = plot(p1,p2,layout=(2,1))
    pB = plot(value.(x),value.(y),ylabel="y",xlabel="x")
    xrange = 0:0.01:2*pi
    ynorth = sin.(xrange) .- wmax
    ysouth = sin.(xrange) .+ wmax
    plot!(xrange,ynorth)
    plot!(xrange,ysouth)
    return pA,pB 
end

pA,pB = river_crossing_direct_transcription()

plot(pB)

******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
 Ipopt is released as open source code under the Eclipse Public License (EPL).
         For more information visit https://github.com/coin-or/Ipopt
******************************************************************************

termination_status = LOCALLY_SOLVED
primal_status      = FEASIBLE_POINT
objective_value    = 1.2798568793864682
Back to top