Stability of hybrid systems
As we have recalled in the recap section on stability of continuous dynamical systems, stability is a property of an equilibrium. But what is an equilibrium of a hybrid systems? It turns out that the definition is not as straightforward as in the continuous case. It also depends on the chosen framework for modelling of hybrid systems.
Equilibrium of a hybrid system modelled by a hybrid automaton
First, an equilibrium of a hybrid automaton is a point \bm x_\mathrm{eq} in the continuous state space \mathcal X\subset \mathbb R^n.
Although we often assume the equilibrium at the origin, that is, \bm x_\mathrm{eq} = \mathbf 0, the assumption does not have to be invoked in order to provide the definition.
We now consider a hybrid automaton for which the dynamics of each individual mode q is given by \dot{\bm x} = \mathbf f_q(\bm x). The invariants (or domains) of each mode are \mathcal X_q, \, q=1, \ldots, m.
The definition of the equilibrium \bm x_\mathrm{eq} that is often found in the literature imposes these two conditions:
- \mathbf 0 = \mathbf f_q(\bm x_\mathrm{eq}) for all q\in \mathcal Q,
- the reset map r(q,q',\bm x_\mathrm{eq}) = \bm x_\mathrm{eq}.
The first condition states that the point in the continuous state space should qualify as an equilibrium for each mode. This might appear unnecessarily restrictive (what if the particular \bm x_\mathrm{eq} is not an element of \mathcal X_q for all q?) as we discuss later. But note that this definition appears in several resources. For example, in the definition 4.9 in the section 4.2 in [1] or the definition 8.2 in the section 8.2 in (no longer available online) [2].
The second condition states that the system can be regarded as resting at the equlibrium even if it jumps from one discrete state (mode) to another (while staying in the equilibrium continuous state).
Equilibrium of a hybrid system modelled by hybrid equations
The state vector within this modelling framework is composed by both the discrete and continuous state variables. The two conditions for the equilibrium of a hybrid automata can be translated into the hybrid equation framework, which means that the equilibrium is not just a single point but rather a set of points.
Example 1 (Equilibrium of a hybrid system modelled by hybrid equations) Consider a hybrid system modelled by hybrid equations, for which the state space is given by \mathcal X = \{0,1\} \times \mathbb R. The dynamics of the system is given by [TBD]
This makes the analysis significantly more challenging. Therefore, in our lecture we will only consider stability of hybrid automata.
Stability of a hybrid automaton
The equilibrium \bm x_\mathrm{eq}=\mathbf 0 is stable if for a given \varepsilon > 0 there exists \delta > 0 such that for all hybrid systems executions/trajectories starting at (q_0,\bm x_0), \|\bm x_0\| < \delta \Rightarrow \|\bm x(\tau)\| < \varepsilon, \; \forall \tau \in \mathcal{T}, where \tau is a hybrid time and \mathcal{T} is the hybrid time domain.
Asymptotic stability
The equilibrium is stable and furthermore we can choose some \delta such that \|\bm x_0\| < \delta \quad \Rightarrow \quad \lim_{\tau\rightarrow \tau_\infty} \|\bm x(\tau)\| = 0, where \tau_\infty<\infty if the execution is Zeno and \tau_\infty=\infty otherwise.
Is stability of the individual dynamics enough?
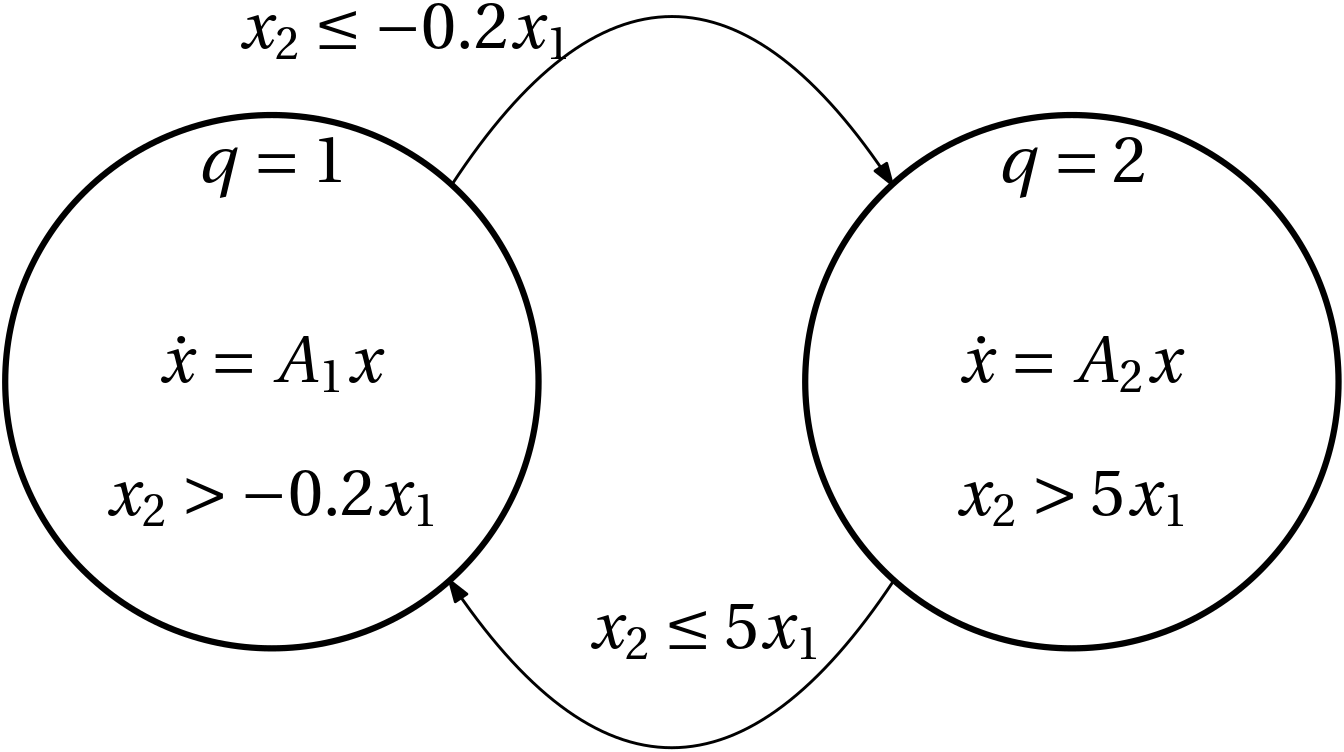
A_1 = \begin{bmatrix} -1 & -100\\ 10 & -1 \end{bmatrix}, \quad A_2 = \begin{bmatrix} -1 & 10\\ -100 & -1 \end{bmatrix}
- Both are stable.
- Switching can be destabilizing.
Can the individual dynamics be unstable?
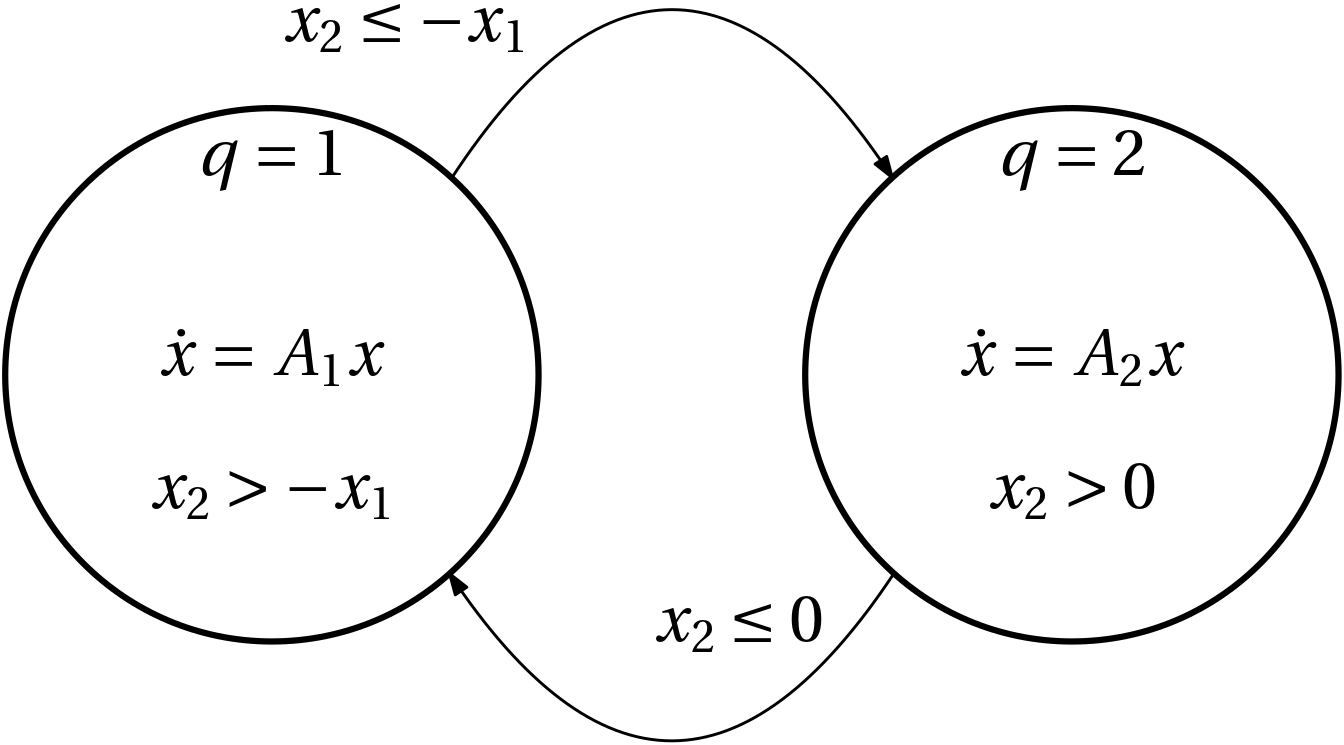
A_1 = \begin{bmatrix} 1 & -100\\ 10 & 1 \end{bmatrix}, \quad A_2 = \begin{bmatrix} 1 & 10\\ -100 & 1 \end{bmatrix}
- Both are unstable.
- Switching can be stabilizing.