Piecewise affine (PWA) systems

This is a subclass of switched systems where the functions on the right-hand side of the differential equations are affine functions of the state. For some (historical) reason these systems are also called piecewise linear (PWL).

We are going to reformulate such systems as switched systems with state-driven switching.

First, we consider the autonomous case, that is, systems without inputs: \dot{\bm x} = \begin{cases} \bm A_1 \bm x + \bm b_1, & \mathrm{if}\, \bm H_1 \bm x + \bm g_1 \leq 0,\\ \vdots\\ \bm A_m \bm x + \bm b_m, & \mathrm{if}\, \bm H_m \bm x + \bm g_m \leq 0. \end{cases}

The nonautonomous case of systems with inputs is then: \dot{\bm x} = \begin{cases} \bm A_1 \bm x + \bm B_1 u + \bm c_1, & \mathrm{if}\, \bm H_1 \bm x + \bm g_1 \leq 0,\\ \vdots\\ \bm A_m \bm x + \bm B_m + \bm c_m, & \mathrm{if}\, \bm H_m \bm x + \bm g_m \leq 0. \end{cases}

Example 1 (Linear system with saturated linear state feedback) In this example we consider a linear system with a saturated linear state feedback as in Fig 1.

Figure 1: Linear system with a saturated linear state feedback

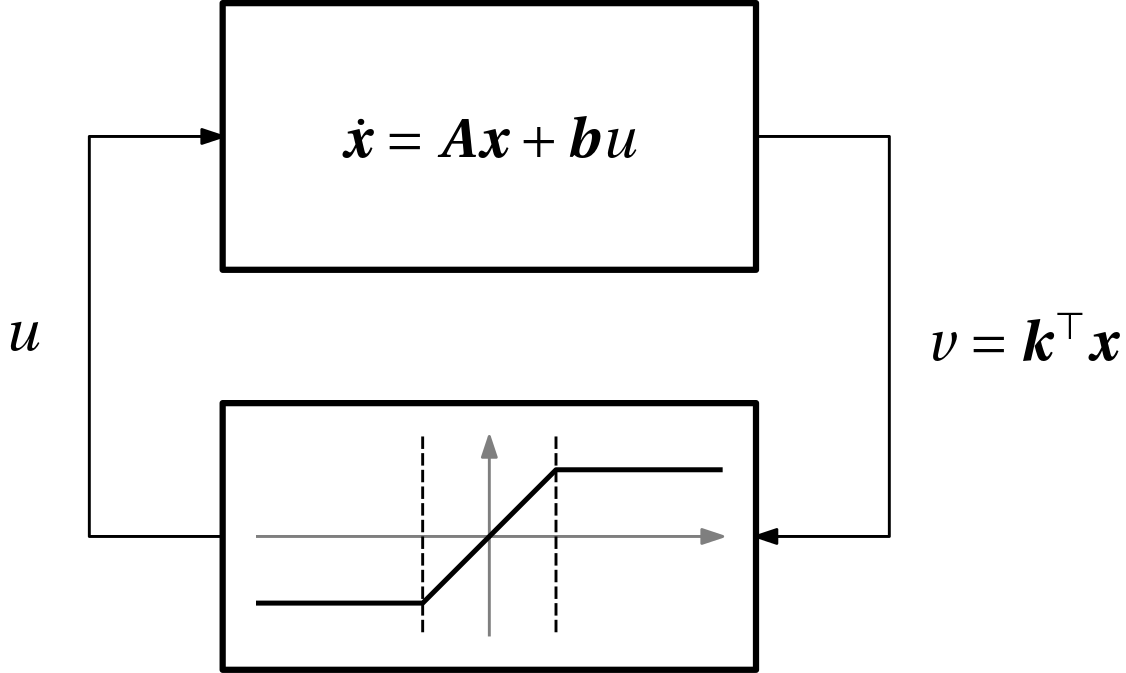
The state equations for the close-loop system are \dot{\bm x} = \bm A\bm x + \bm b \,\mathrm{sat}(v), \quad v = \bm k^T \bm x, which can be reformulated as a piecewise affine system \dot{\bm x} = \begin{cases} \bm A \bm x - \bm b, & \mathrm{if}\, \bm x \in \mathcal{X}_1,\\ (\bm A + \bm b \bm k^\top )\bm x, & \mathrm{if}\, \bm x \in \mathcal{X}_2,\\ \bm A \bm x + \bm b, & \mathrm{if}\, \bm x \in \mathcal{X}_3,\\ \end{cases} where the partitioning of the space of control inputs is shown in Fig 2.

Figure 2: Partitioning the control input space

Expressed in the state space, the partitioning is \begin{aligned} \mathcal{X}_1 &= \{\bm x \mid \bm H_1\bm x + g_1 \leq 0\},\\ \mathcal{X}_2 &= \{\bm x \mid \bm H_2\bm x + \bm g_2 \leq 0\},\\ \mathcal{X}_3 &= \{\bm x \mid \bm H_3\bm x + g_3 \leq 0\}, \end{aligned} where \begin{aligned} \bm H_1 &= \bm k^\top, \quad g_1 = 1,\\ \bm H_2 &= \begin{bmatrix}-\bm k^\top\\\bm k^\top\end{bmatrix}, \quad \bm g_2 = \begin{bmatrix}-1\\-1\end{bmatrix},\\ \bm H_3 &= -\bm k^\top, \quad g_3 = 1. \end{aligned}

Approximation of nonlinear systems

While the example with the saturated linear state feedback can be modelled as a PWA system exactly, there are many practical cases, in which the system is not exactly PWA affine but we want to approximate it as such.

Example 2 (Nonlinear system approximated by a PWA system) Consider the following nonlinear system \begin{bmatrix} \dot x_1\\\dot x_2 \end{bmatrix} = \begin{bmatrix} x_2\\ -x_2 |x_2| - x_1 (1+x_1^2) \end{bmatrix}

Our task is to approximate this system by a PWA system. Equivalently, we need to find a PWA approximation for the right-hand side function.