Solution concepts
Now that we know how to model hybrid systems, we need to define what we mean by a solution to a hybrid system. The definitions are not as straightforward as in the continuous-time or discrete-time case and mastering them is not only of theoretical value.
Hybrid time and hybrid time domain
Even before we start discussing the concepts of a solution, we need to discuss the concept of time in hybrid systems. Of course, hybrid systems live in the same world as we do, and therefore they evolve in the same physical time, but it turns out that we can come up with an artificial concept of hybrid time that makes modelling and analysis of hybrid systems convenient.
Recall that in continuous-time systems, the continuous time t\in\mathbb R_{\geq 0}, and in discrete-time systems, the discrete “time” k\in\mathbb N. We put the latter in quotation marks since k is not really the time but rather it should be read as the kth transition of the system. Now, the idea is to combine these two concepts of time into one, and we call it the hybrid time (t,j), \; t\in \mathbb R_{\geq 0},\, j\in \mathbb N.
If you think that it is redundant, note that since hybrid systems can exhibit discrete-event system behaviour, a transition from one discrete state to another can happen instantaneously. In fact, several such transitions can take no time at all. It sounds weird, but that is what the mathematical model allows. That is why determining t need not be enough and we also need to specify j.
The set of all hybrid times for a given hybrid system is called hybrid time domain E \subset [0,T] \times \{0,1,2,\ldots, J\}, where T and J can be finite or \infty.
In particular, E = \bigcup_{j=0}^J \left([t_j,t_{j+1}] \times \{j\}\right) \tag{1}
where 0=t_0 < t_1 < \ldots < t_J = T.
The meaning of Eq. 1 can be best explained using Fig. 1 below.
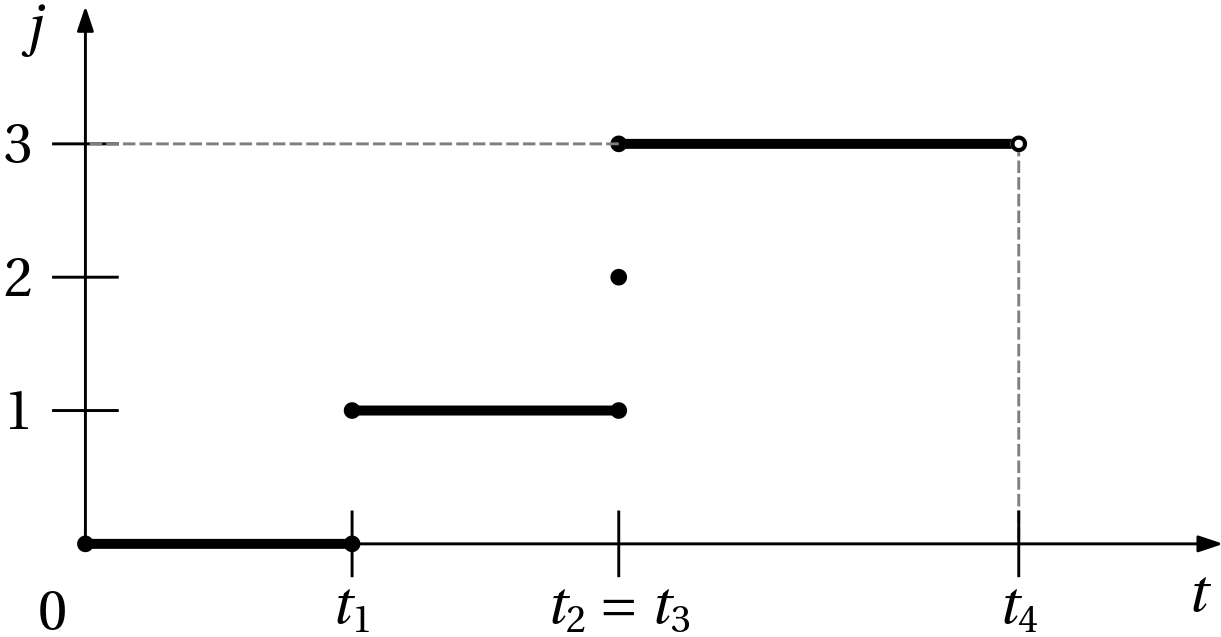
Note that if two hybrid times are from the same hybrid domain, we can decide if (t,j) \leq (t',j'). In other words, the set of hybrid times is totally ordered.
Hybrid arc
Hybrid arc is just a terminology used in the literature for hybrid state trajectory. It is a function that assigns a state vector x to a given hybrid time (t,j) x: E \rightarrow \mathbb R^n.
For each j the function t \mapsto x(t,j) is absolutely continuous on the interval I^j = \{t \mid (t,j) \in E\}.
We admit here that we are not going to be 100% consistent in the usage of the notation x(t,j) in the rest of our course. Oftentimes use x(t) even within hybrid systems when we do not need to index the jumps.
It is perhaps clear now, that hybrid time domain can only be determined once the solution (the arc, the trajectory) is known. This is in sharp contrast with the continuous-time or discrete-time system – we can formulate the problem of finding solution to \dot x(t) = 3x(t), \, x(0) = 1 on the interval [0,2], where the interval was set even before we know how the solution looks like.
Solutions of autonomous (no-input) systems
Finally we can formalize the concept of a solution. A hybrid arc x(\cdot,\cdot) is a solution to the hybrid equations given by the common quadruple \{\mathcal{C},\mathcal{D},f,g\} (or \{\mathcal{C},\mathcal{D},\mathcal{F},\mathcal{G}\} for inclusions), if
- the initial state x(0,0) \in \overline{\mathcal{C}} \cup \mathcal{D}, and
- for all j such that I^j = \{t\mid (t,j)\in E\} has a nonempty interior \operatorname{int}I^j
- x(t,j) \in \mathcal C \; \forall t\in \operatorname{int}I^j,
- \dot x(t,j) = f(x(t,j)) \; \text{for almost all}\; t\in I^j, and
- for all (t,j)\in E such a (t,j+1)\in E
- x(t,j) \in \mathcal{D}, and
- x(t,j+1) = g(x(t,j)).
Make the modifications for the \{\mathcal{C},\mathcal{D},\mathcal{F},\mathcal{G}\} version by yourself.
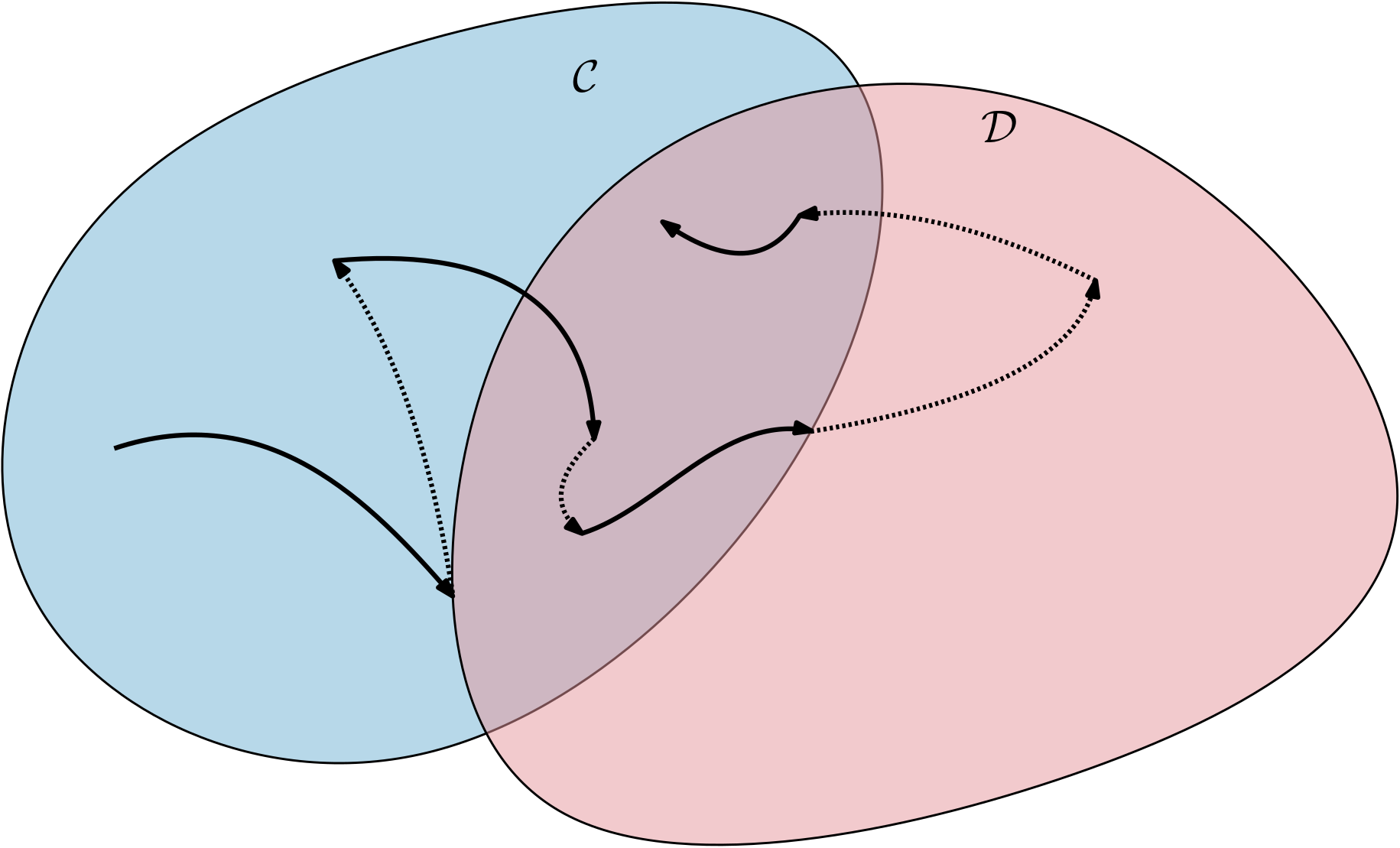
Example 1 (Solution) An example of a solution is in Fig. 2. Follow the solution with your finger and make sure you understand what and why is happening. In particular, in the overlapping region, the solution is not unique. While it can continue flowing, it can also jump.
Hybrid input
Similarly as we considered the state as a function of the hybrid time, we can consider the input as a function of the hybrid time. With its own hybrid domain E_\mathrm{u}, the input is u: E_\mathrm{u} \rightarrow \mathbb R^m.
For each j the function t \mapsto u(t,j) must be… well-behaved… For example, piecewise continuous on the interval I^j = \{t \mid (t,j) \in E_\mathrm{u}\}.
Solutions of systems with inputs
We assume that hybrid time domains for the arcs and inputs are the same. A solution must satisfy the same conditions as in the case of autonomous systems, but with the input taken into account. For completeness we state the conditions here:
- The initial state-control pair (x(0,0),u(0,0)) \in \overline{\mathcal{C}} \cup \mathcal{D}, and
- for all j such that I^j = \{t\mid (t,j)\in E\} has a nonempty interior \operatorname{int}I^j
- (x(t,j),u(t,j)) \in \mathcal C \; \forall t\in \operatorname{int}I^j,
- \dot x(t,j) = f(x(t,j),u(t,j)) \; \text{for almost all}\; t\in I^j, and
- for all (t,j)\in E such a (t,j+1)\in E
- (x(t,j),u(t,j)) \in \mathcal{D}, and
- x(t,j+1) = g(x(t,j),u(t,j)).