Timed Petri nets
Recall that when introducing enabled transitions, we emphasized that these can but do not have to fire immediately after having been enabled \boxed{\mathrm{ENABLING} \neq \text{FIRING}.}
Delays associated with transitions
Well then, the enabled transitions do not have to fire immediately, but they can possibly fire with some delay after enabling. This is for the first time that we are introducing the concept of time into the Petri nets, isn’t it?
For the jth transition, the delay of the kth firing is v_{j,k}, and we collect the sequence of delayes into v_j = \{v_{j,1}, v_{j,2}, \ldots \}.
But not all transitions have to be timed. Denote the timed transitions \mathcal{T}_\mathrm{D}\subseteq \mathcal{T}. We define the clock structure for a PN as \mathcal{V} = \{v_j\mid t_j\in\mathcal{T}_\mathrm{D}\}.
The definition of a timed Petri net (TPN) is then obtained by augmenting the definition of a Petri net with the clock structure
\boxed{TPN = \{\mathcal{P}, \mathcal{T}, \mathcal{A}, w, x, \mathcal{V}\}}.
Example 1 (Timed Petri net) Model of processing multiple tasks: task 1 and task 2 are processed sequentially, and task 3 is processed in parallel with them; task 4 can only be processed after both tasks 2 and 3 have been finished. Finishing individual tasks corresponds to the individual transitions. The transition 4 is untimed, it only expresses the logical requirement.
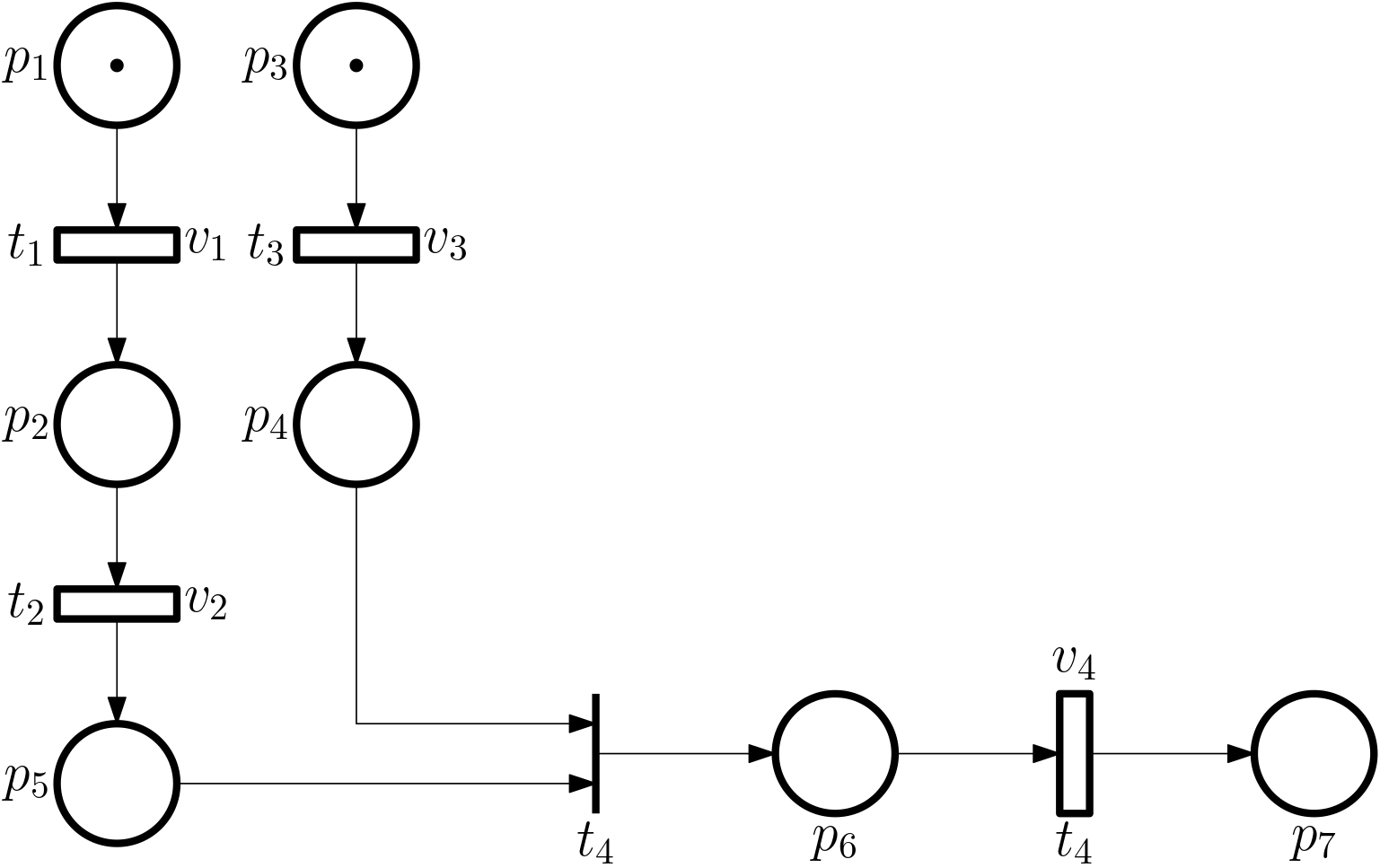
Sometimes instead of a bar, the untimed transitions are modelled using similarly thin rectangles as the timed transitions, but filled.
Places can also be delayed
With delays associated with just one type of a node in a Petri net, the situation is rather nonsymmetric. In some literature, delays can also associated with places. And yet in some other literature delays are only associated with places. Such delays associated with places are called holding time for a place It is the minimum duration the token must rest in the place. But the token can stay longer if the output transition is waiting for other places.
There is a major difference in delays associated with places compared to the delays associated with transitions. While the former tells the minimum duration the token has to dwell in the place, the latter tell the exact delay with which the transition fires after having been enabled.
Timed Petri net dynamics
With the introduction of time into the Petri nets, we can now study the dynamics of the system. For general Petri nets, alhough perfectly doable, it may quicly become too complex, and therefore here we only consider event graphs.
Some notation:
- \{\tau_{j,1}, \tau_{j,2}, \ldots\} are the firing times of the jth transition,
- \{\pi_{i,1},\pi_{i,2},\ldots\} are the times when the ith place receives a token,
- x_i = x(p_i) is the number of tokens at the ith place,
- x_{i,k} = \left.x(p_i)\right|_k, is the number of tokens at the ith place after the kth firing.
Now, assume first that x_{i,0} = 0. We can then relate the time of the arrival of the token to the place with the firing of the transition from which the token arrives \pi_{i,k} = \tau_{j,k},\quad p_i\in \mathcal{O}(t_j).
But generally x_{i,0} \neq 0 and the above relation needs to be modified to \pi_{i,k+x_{i,0}} = \tau_{j,k},\quad p_i\in \mathcal{O}(t_j), or, equivalently \boxed{\pi_{i,k} = \tau_{j,k-x_{i,0}},\quad p_i\in \mathcal{O}(t_j).} \tag{1}
This can be read in the following way. If there are initially, say, 3 tokens in the place, the time of the arrival of the 4th token is the time of the first firing of the transition from which the 4th token arrives.
Good. Keep this result in mind. Now we go for another.
For an untimed transition with a single input place, the firing time is the same as the time of the arrival of the token to the place \tau_{j,k} = \pi_{i,k}.
Modifying this result for a timed transition with a single input place we get \tau_{j,k} = \pi_{i,k} + v_{j,k}.
In words, the firing time is given by the time of the arrival of the token to the place, which enables the transition, and the delay associated with the transition.
Finally, we extend this result to the case of a timed transition with multiple input places \boxed{ \tau_{j,k} = \max_{p_i\in\mathcal{I}(t_j)}\{\pi_{i,k}\} + v_{j,k}.} \tag{2}
This is the other promised important result. Keep both boxed formulas Eq. 1 and Eq. 2 handy, they will be needed in what is coming.
Example 2 (Timed Petri net dynamics) Consider the Petri net with three places and two transitions, one of which is timed, as in Fig. 1.
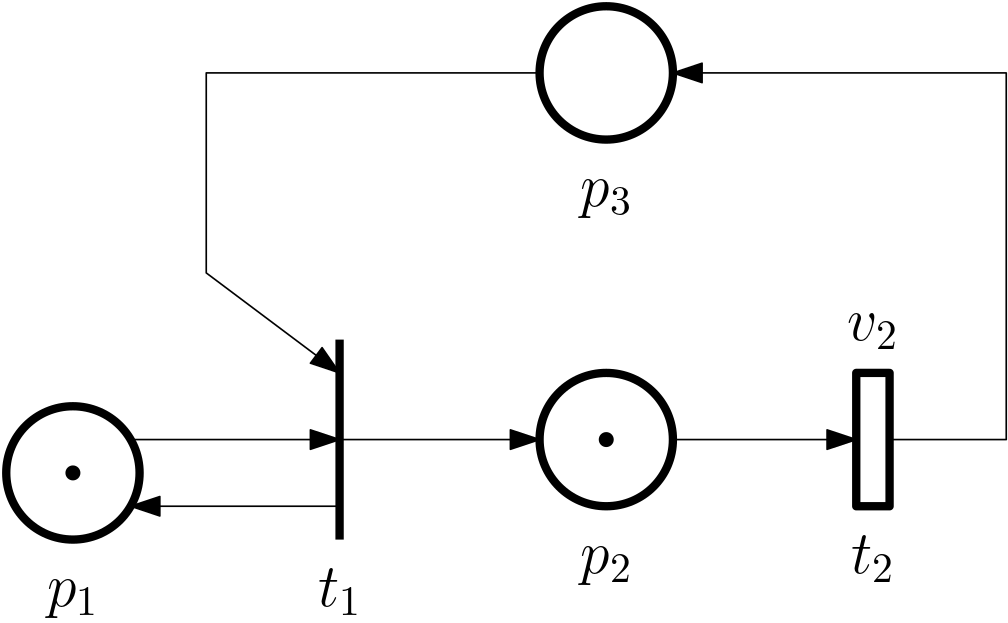
We first use Eq. 2 to write down the firing times of the two transitions \begin{aligned} \tau_{1,k} &= \max\{\pi_{1,k},\pi_{3,k}\}\\ \tau_{2,k} &= \pi_{2,k}+v_{2,k}. \end{aligned}
Now we apply Eq. 1 to write down the times of the arrival of the tokens to the places \begin{aligned} \pi_{1,k} &= \tau_{1,k-1}, \qquad k=2,\ldots, \qquad \pi_{1,0} = 0\\ \pi_{2,k} &= \tau_{1,k-1}, \qquad k=2,\ldots, \qquad \pi_{2,0} = 0\\ \pi_{3,k} &= \tau_{2,k}, \qquad k=1,\ldots \end{aligned}
Substituting from the latter into the former we get \begin{aligned} \tau_{1,k} &= \max\{\tau_{1,k-1},\tau_{1,k-1}+v_{2,k}\}\\ &= \tau_{1,k-1}+v_{2,k}, \quad \tau_{1,k} = 0\\ \tau_{2,k} &= \tau_{1,k-1}+v_{2,k}. \end{aligned}
This is the ultimate model for the dynamics of the Petri net. Should we need it, we can also get similar expressions for the times of the arrival of the tokens to the places.
While with state equations we compute a sequences of values of the state vector (\bm x_0, \bm x_1, \bm x_2, \ldots), in other words, we compute the evolution of the state in time, here we compute the sequences of times when transitions fire (or token arrive to places). This update scheme for times resembles the state equations, but the interpretation is different.
Queueing system using TPN
We can also model a queueing system using a TPN. The Petri net is shown in Fig. 2.
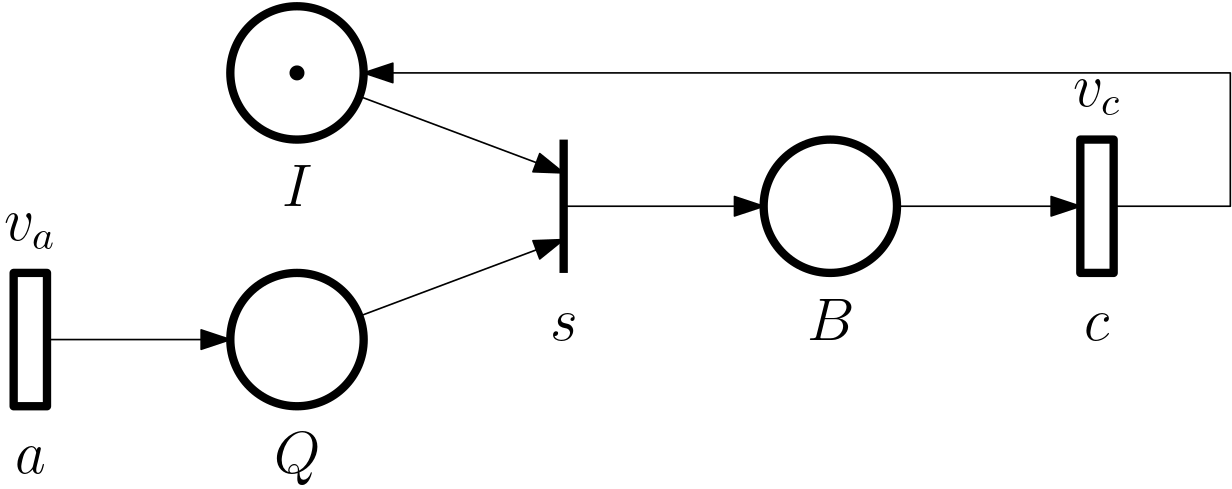
Of the three transitions \mathcal{T} = \{a,s,c\}, which we have already identified previously, we assume that only are times, namely \mathcal{T}_\mathrm{D} = \{a,c\}. The associated firing delays are \bm v = \begin{bmatrix}v_a \\ v_c\end{bmatrix}.
For convenience we relabel the firing times of the transitions. Instead of t_{a,k} we will use a_k, and similarly s_k, and c_k. Application of Eq. 2 and Eq. 1 gives \begin{aligned} a_k &= a_{k-1} + v_{a,k},\quad k=1,2,\ldots,\quad a_0 = 0\\ s_k &= \max\{\pi_{Q,k},\pi_{I,k}\}\\ c_k &= \pi_{B,k} + v_{c,k}\\ \pi_{Q,k} &= a_{k},\quad k=1,2,\ldots\\ \pi_{I,k} &= c_{k-1},\quad k= 2, \ldots, \quad \pi_{I,0}=1\\ \pi_{B,k} &= s_{k},\quad k=1,2,\ldots\\ \end{aligned}
Combining gives the desired update equations \begin{aligned} a_k &= a_{k-1} + v_{a,k},\quad k=1,2,\ldots,\quad a_0 = 0\\ s_k &= \max\{a_{k},c_{k-1}\}\\ c_k &= s_{k} + v_{c,k}\\ &= \max\{a_{k},c_{k-1}\} + v_{c,k},\quad k=1,\ldots, \quad c_0=0 \end{aligned}
The time of completing the kth task is given by the time at which the previous task was completed and the time needed to complete the kth task itself, unless there is a gap in the queue after finishing the previous task, in which case the server must wait for the next task to arrive.
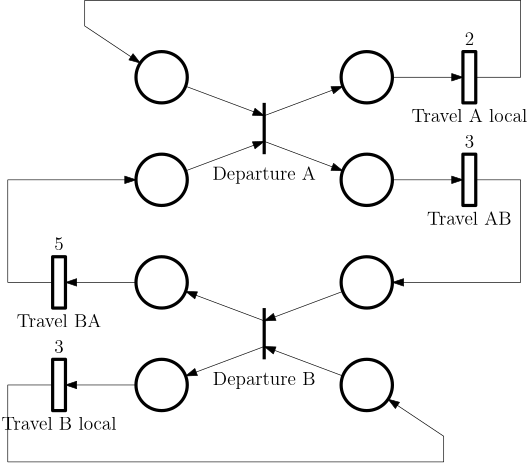
Example 3 (Timed Petri net for synchronization of train lines) We consider three closed rail tracks and two stations as in Fig. 3.
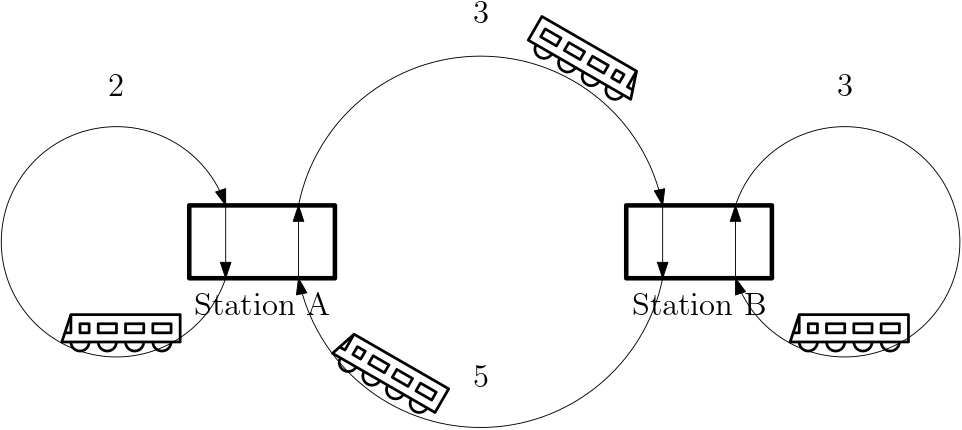
Departure of a train at a station must be synchronized with arrival of the other train so that passengers can change train. The timed Petri net for this system is shown in Fig. 4.
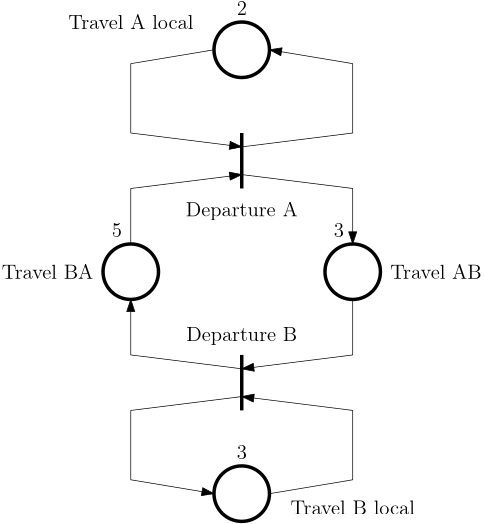
If time is associated with the places, the Petri net simplifies significantly to Fig. 5.
Example 4 (Manufacturing) tbd
Extensions
Stochastic Petri nets (SPN)
Numerous extensions are possible, some of which we have already mentioned when discussing untimed Petri nets. But upon introducing time, stochastic Petri nets can be conceived, in which delays are random variables.