State automata

Having just discussed the concept of a discrete-event system, we now introduce the most popular modeling framework for such systems: a state automaton, or just an automaton (plural automata). It is also known as a state machine or a (discrete) transition system.

Definition 1 (Automaton) Automaton is a tuple \boxed{ G = \{\mathcal X,\mathcal X_0,\mathcal E,\mathcal F\},}
where

  • \mathcal X is the set of states (also called modes or locations).
  • \mathcal X_0 \subseteq \mathcal X is the set of initial states.
  • \mathcal E is the set of events (also actions, transition labels, symbols). It is also called alphabet.
  • \mathcal F\subseteq \mathcal X \times \mathcal E \times \mathcal X is the set of transitions. In the deterministic case it can also be narrowed down to a transition function f:\mathcal X \times \mathcal E \rightarrow \mathcal X. Note that f is then is a partial function, it is not necessarily defined for all combinations of states and events. Sometimes f is used even for multivalued functions: f:\mathcal X \times \mathcal E \rightarrow 2^\mathcal{X}, where 2^\mathcal{X} is a power set (a set of all subsets of X).
Some comments on the notation
  • The set of states is often denoted by \mathcal Q to spare the letter \mathcal X for the continuous valued state space of hybrid systems.
  • The set of events is often denoted by \mathcal A to spare the letter \mathcal E for the set of transitions (edges in the corresponding graph), because F and f may also need to be spared for the continuous-valued transitions. But then the letter \mathcal A actually fits this purpose nicely because the event set is also called the alphabet.

Marked states

In some literature, the definition of the automaton also includes a set \mathcal X_\mathrm{m} \subseteq \mathcal X of marked or accepting states, in which case the definition of an automaton now includes three (sub)sets of states: \mathcal X, \mathcal X_0 and \mathcal X_\mathrm{m}. \boxed{ G = \{\mathcal X,\mathcal X_0,\mathcal E,\mathcal F, \mathcal X_\mathrm{m}\}.}

The marked states are just some states with special roles in the system. Namely, these are the states into which the system should be controlled. I do not particularly like this idea of mixing the model of the system with the requirements, but some part of the community likes it this way.

Automaton as a (di)graph (also a state transition diagram)

So far the definition of an automaton was not particularly visual. This can be changes by viewing the automaton as a directed graph (digraph) with. These are the basic rules

  • State is represented as a node of the graph.
  • Transition from a given state to another state is represented as an edge connecting the two nodes.
  • Events (actions) are the labels attached to the edges. It is not necessary that each edge has its unique label.

Example 1 (Automaton as a digraph) Consider an automaton defined by these sets: \mathcal X = \{x_1,x_2,x_3\}, \mathcal X_0 = \{x_1\}, \mathcal E = \{e_1,e_2,e_3\}, \mathcal F = \{(x_1,e_1,x_2),(x_2,e_2,x_1),(x_1,e_3,x_3),(x_2,e_2,x_3)\}.

The corresponding digraph is in Fig 1.

G init init x₁ x₁ init->x₁ x₂ x₂ x₁->x₂ e₁ x₃ x₃ x₁->x₃ e₂ x₂->x₁ e₂ x₂->x₃ e₃
Figure 1: An example automaton as a digraph

We may also encounter the following term.

Definition 2 (Active event function and set) Active event function (actually a multivalued function) \Gamma: \mathcal X \rightarrow 2^\mathcal{E} assigns to each state a set of active events. Active event set \Gamma(x) is the set of active events in a particular state x.

Finite state automaton (FSA)

This may be regarded as a rather superfluous definition – a finite state automaton (FSA) is a state automaton with a finite set \mathcal X of states. It is also known as a finite state machine (FSM).

Execution of an automaton

  • x_1\xrightarrow{e_1} x_2\xrightarrow{e_2} x_1 \xrightarrow{e_1} x_2 \xrightarrow{e_4} x_3\ldots
  • Sometimes also written as x_1,e_1,x_2,e_2,\ldots
Notational confusion

Here x_k for some k is the name of a particular state. It is not the name of a (yet to be introduced) state variable; In fact, it can be viewed as its value (also valuation).

  • Some authors strictly distinguish between the state variable and the state (variable valuation),
    • similarly as in probability theory random variable X vs its value x, as in F(x) = P(X\leq x);
  • some do not, but then it may lead to confusion;
  • yet some others avoid the problem by not introducing state variables and only working with enumerated states.
Notational confusion 2

Even worse, it is also tempting to interpret the lower index k as (discrete) time, but nope, in the previous k is not the time index.

Again, some authors do not distinguish…

Path of an automaton

Corresponding to the execution

x_1\xrightarrow{e_1} x_2\xrightarrow{e_2} x_1 \xrightarrow{e_1} x_2 \xrightarrow{e_4} x_3\ldots

the path is just the sequence of visited states:

x_1,x_2,x_1,x_2,x_3,\ldots

In continuous-valued dynamical systems, we have a state trajectory, but then time stamps are attached to each visited state.

Example 2 (Beverage vending machine)  

G init init waiting waiting init->waiting swiped swiped waiting->swiped swipe card swiped->waiting reject payment paid paid swiped->paid accept payment coke_dispensed coke_dispensed paid->coke_dispensed choose coke fanta_dispensed fanta_dispensed paid->fanta_dispensed choose fanta coke_dispensed->waiting take coke fanta_dispensed->waiting take fanta
Figure 2: Example of a digraph representation of the automaton for a beverage vending machine

  • State sequence (path): waiting, swiped, paid, coke_dispensed, waiting

  • Events sequence: swipe card, accept payment, choose coke, take coke

  • Indeed, the two states coke_dispensed and fanta_dispensed can be merged into just beverage_dispensed.

  • How about other paths? Longer? Shorter?

G init init waiting waiting init->waiting swiped swiped waiting->swiped swipe card swiped->waiting reject payment paid paid swiped->paid accept payment coke_dispensed coke_dispensed paid->coke_dispensed choose coke fanta_dispensed fanta_dispensed paid->fanta_dispensed choose fanta coke_dispensed->waiting take coke fanta_dispensed->waiting take fanta
Figure 3: Example of a digraph representation of the automaton for a beverage vending machine with a marked state

The waiting state can be marked (is accepting).

Example 3 (Longitudinal control of a ground vehicle)  

G init init still still init->still accelerating accelerating still->accelerating push acc cruising cruising accelerating->cruising cruise ON coasting coasting accelerating->coasting rel acc cruising->accelerating push acc cruising->coasting rel acc braking braking cruising->braking push brake coasting->braking push brake braking->still zero vel braking->cruising cruise ON braking->coasting rel brake
Figure 4: Example of a digraph representation of the automaton for a longitudinal control of a ground vehicle
  • By cruise on I mean switching on some kind of a cruise control system, which keeps the velocity constant.
  • It turns out the optimal control strategy for trains (under some circumstances).
  • Note that some of the events are indeed actions started by the driver, but some are just coming from the physics of the vehicle (transition from braking to zero velocity).

Example 4 (Corridor switch)  

G init init OFF OFF init->OFF ON ON OFF->ON switch₁,switch₂ ON->OFF switch₁,switch₂
Figure 5: Example of a digraph representation of the automaton for a corridor switch

Two events associated with one transitions can be seen as two transitions, each with a single event, both sharing the starting and ending states.

Example 5 (JK flip-flop) We now consider the classical JK flip-flop logical circuit. It symbol is in Fig 7 and the truth table follows. Our goal is to represent its functionality using a state automaton.

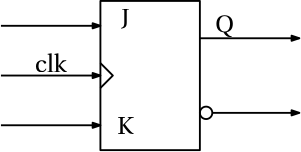
Figure 6: Symbol for a JK flip-flop logical circuit
J K Q_k Q_{k+1} Description
0 0 0 0 No change
0 0 1 1 No change
0 1 0 0 Reset
0 1 1 0 Reset
1 0 0 1 Set
1 0 1 1 Set
1 1 0 1 Toggle
1 1 1 0 Toggle
G init init Low Low init->Low Low->Low ¬J ∧ ¬K ∧ clk High High Low->High J ∧ clk High->Low K ∧ clk High->High ¬J ∧ ¬K ∧ clk
Figure 7: JK flip-flop as an automaton

Example 6 (Double intensity switching)  

G init init OFF OFF init->OFF ON ON OFF->ON push ON->OFF push ON2 ON2 ON->ON2 push ON2->OFF push
Figure 8: Example of a digraph representation of the automaton for double intensity switching

Obviously we need to introduce time into the automaton…

State as the value of a state variable

Definition of the state space by enumeration (such as \mathcal X = \{0,1,2,3,4,5\}) doesn’t scale well. As an alternative, a state can be characterized by the value (sometimes also valuation) of a state variable. A state variable is then given by

  • the name (for example, x),
  • the “type” (boolean, integer, vector, …).

Example 7 (Examples of state variables)  

  • Corridor switch: x \in \{\mathrm{false},\mathrm{true}\} (possibly also \{0,1\}).
  • Double intensity switching:
    • x \in \{0,1,2\} \subset \mathbb Z,
    • or \bm x = \begin{bmatrix}x_1\\ x_2 \end{bmatrix}, where x_1,x_2 \in \{0,1\}.

State (transition) equation

Denoting a new state after a transition as x^+, the state equation reads \boxed{x^+ = f(x,e)}

Upon introduction of discrete-time (index) k, it can also be rewritten as x_{k+1} = f(x_k,e_k) or also x[k+1] = f(x[k],e[k]).

Note
  • The function f can be defined by a computer code rather than a clean mathematical formula.
  • The discrete-time index of the event is sometimes considered shifted, that is x_{k+1} = f(x_k,e_{k+1}). You should be aware of this.

Extensions

The concept of an automaton can be extended in several ways. In particular, the following two extensions introduce the concept of an output to an automaton.

Moore machine

One extension of an automaton with outputs is Moore machine. The outputs assigned to the states by the output function y = g(x).

The output is produced (emitted) when the (new) state is entered.

Note, in particular, that the output does not depend on the input. This has a major advantage when a feedback loop is closed around this system, since no algebraic loop is created.

Graphically, we make a conventions that outputs are the labels of the states.

Example 8 (Moore machine) The following automaton has just three states, but just two outputs (FLOW and NO FLOW).

G init init closed NO FLOW Valve closed init->closed partial FLOW Valve partially open closed->partial open valve one turn partial->closed close valve one turn full FLOW Valve fully open partial->full open valve one turn full->closed emergency shut off full->partial close valve one turn
Figure 9: Example of a digraph representation of the Moore machine for a valve control

Mealy machine

Mealy machine is another extension of an automaton. Here the outputs are associated with the transitions rather than the states.

Since the events already associated with the states can be viewed as the inputs, we now have input/output transition labels. The transition label e_\mathrm{i}/e_\mathrm{o} on the transion from x_1 to x_2 reads as “the input event e_\mathrm{i} at state x_1 activates the transition to x_2, which outputs the event e_\mathrm{o}” and can be written as x_1\xrightarrow{e_\mathrm{i}/e_\mathrm{o}} x_2.

It can be viewed as if the output function also considers the input and not only the state y = e_\mathrm{o} = g(x,e_\mathrm{i}).

In contrast with the Moore machine, here the output is produced (emitted) during the transition (before the new state is entered).

Example 9 (Mealy machine) Coffee machine: coffee for 30 CZK, machine accepting 10 and 20 CZK coins, no change.

G init init 0 No coin init->0 10 10 CZK 0->10 insert 10 CZK / no coffee 20 20 CZK 0->20 insert 20 CZK / no coffee 10->0 insert 20 CZK / coffee 10->20 insert 10 CZK / no coffee 20->0 insert 10 CZK / coffee 20->10 insert 20 CZK / coffee
Figure 10: Example of a digraph representation of the Mealy machine for a coffee machine

Example 10 (Reformulate the previous example as a Moore machine) Two more states wrt Mealy

G init init 0 NO COFFEE No coin init->0 10 NO COFFEE 10 CZK 0->10 insert 10 CZK 20 NO COFFEE 20 CZK 0->20 insert 20 CZK 10->20 insert 10 CZK 30 COFFEE 10+20 CZK 10->30 insert 20 CZK 20->30 insert 10 CZK 40 COFFEE 20+20 CZK 20->40 insert 20 CZK 30->0 30->10 insert 10 CZK 30->20 insert 20 CZK 40->10 40->20 insert 10 CZK 40->30 insert 20 CZK
Figure 11: Example of a digraph representation of the Moore machine for a coffee machine
Note

There are transitions from 30 and 40 back to 0 that are not labelled by any event. This does not seem to follow the general rule that transitions are always triggered by events. Not what? It can be resolved upon introducing time as the timeout transitions.

Example 11 (Dijkstra’s token passing) The motivation for this example is to show that it is perhaps not always productive to insist on visual description of the automaton using a graph. The four components of our formal definition of an automaton are just enough, and they translate directly to a code.

The example comes from the field of distributed computing systems. It considers several computers that are connected in ring topology, and the communication is just one-directional as Fig 12 shows. The task is to use the communication to determine in – a distributed way – which of the computers carries a (single) token at a given time. And to realize passing of the token to a neighbour. We assume a synchronous case, in which all the computers are sending simultaneously, say, with some fixed sending period.

G 0 0 1 1 0->1 2 2 1->2 3 3 2->3 3->0
Figure 12: Example of a ring topology for Dijkstra’s token passing in a distributed system

One popular method for this is called Dijkstra’s token passing. Each computer keeps a single integer value as its state variable. And it forwards this integer value to the neighbour (in the clockwise direction in our setting). Upon receiving the value from the other neighbour (in the counter-clockwise direction), it updates its own value according to the rule displayed in the code below. At every clock tick, the state vector (composed of the individual state variables) is updated according to the function update!() in the code. Based on the value of the state vector, an output is computed, which decodes the informovation about the location of the token from the state vector. Again, the details are in the output() function.

Show the code 
struct DijkstraTokenRing
    number_of_nodes::Int64
    max_value_of_state_variable::Int64
    state_vector::Vector{Int64}
end

function update!(dtr::DijkstraTokenRing)                        
    n = dtr.number_of_nodes
    k = dtr.max_value_of_state_variable
    x = dtr.state_vector
    xnext = copy(x)
    for i in eachindex(x)   # Mind the +1 shift. x[2] corresponds to x₁ in the literature.
        if i == 1                                              
            xnext[i] = (x[i] == x[n]) ? mod(x[i] + 1,k) : x[i]  # Increment if the left neighbour is identical.
        else                                                    
            xnext[i] = (x[i] != x[i-1]) ? x[i-1] : x[i]         # Update by the differing left neighbour.
        end
    end
    dtr.state_vector .= xnext                                              
end

function output(dtr::DijkstraTokenRing)     # Token = 1, no token = 0 at the given position. 
    x = dtr.state_vector
    y = similar(x)
    y[1] = iszero(x[1]-x[end])
    y[2:end] .= .!iszero.(diff(x))
    return y
end
output (generic function with 1 method)

We now rund the code for a given number of computers and some initial state vector that does not necessarily comply with the requirement that there is only one token in the ring.

Show the code 
n = 4                           # Concrete number of nodes.
k = n                           # Concrete max value of a state variable (>= n).
@show x_initial = rand(0:k,n)   # Initial state vector, not necessarily acceptable (>1 token in the ring).
dtr = DijkstraTokenRing(n,k,x_initial)
@show output(dtr)               # Show where the token is (are).

@show update!(dtr), output(dtr) # Perform the update, show the state vector and show where the token is.
@show update!(dtr), output(dtr) # Repeat a few times to see the stabilization.    
@show update!(dtr), output(dtr)
@show update!(dtr), output(dtr)
@show update!(dtr), output(dtr)
x_initial = rand(0:k, n) = [1, 3, 0, 2]
output(dtr) = [0, 1, 1, 1]
(update!(dtr), output(dtr)) = ([1, 1, 3, 0], [0, 0, 1, 1])
(update!(dtr), output(dtr)) = ([1, 1, 1, 3], [0, 0, 0, 1])
(update!(dtr), output(dtr)) = ([1, 1, 1, 1], [1, 0, 0, 0])
(update!(dtr), output(dtr)) = ([2, 1, 1, 1], [0, 1, 0, 0])
(update!(dtr), output(dtr)) = ([2, 2, 1, 1], [0, 0, 1, 0])
([2, 2, 1, 1], [0, 0, 1, 0])

We can see that although initially the there can be more tokens, after a few iterations the algorithm achieves the goal of having just one token in the ring.

Extended-state automaton

Yet another extension of an automaton is the extended-state automaton. And indeed, the hyphen is there on purpose as we extend the state space.

In particular, we augment the state variable(s) that define the states/modes/locations (the nodes in the graph) by additional (typed) state variables: Int, Enum, Bool, …

Transitions from one mode to another are then guarded by conditions on theses new extra state variables.

Besides being guarded by a guard condition, a given transition can also be labelled by a reset function that resets the extended-state variables.

Example 12 (Counting up to 10) In this example, there are two modes (on and off), which can be captured by a single binary state variable, say x. But then there is an additional integer variable k, and the two variables together characterize the extended state.

G init init OFF OFF init->OFF int k=0 ON ON OFF->ON press ON->OFF (press ⋁ k ≥ 10); k=0 ON->ON (press ∧ k < 10); k=k+1
Figure 13: Example of a digraph representation of the extended-state automaton for counting up to ten

Composing automata

Any practically useful modelling framework should support decomposition of a large system into smaller subsystems. These should then be able to communicate/synchronize with each other. In automata such synchronization can be realized by sending (or generating) and receiving (or accepting) events. A common choice of symbols for the two is !,?, as illustrated in the following example. But these symbols are just one possible convention, and any other symbols can be used.

Example 13 (Composing automata)  

G init init 1 1 init->1 2 2 1->2 press? 3 3 3->3 press!
Figure 14: Example illustrating how two automata can be synchronized by sending and receiving events

Languages and automata

When studying automata, we often encounter the concept of a language. Indeed, the concept of an automaton is heavily used in the formal laguage theory. Although in our course we are not going to refer to these results, some resources we recommend for our courses do, and so it is useful to understand how automata and languages are related.

First, we extend the definition of a transition function in that it accepts the current state and not just a single event but a sequence of events, that is

f: \mathcal X \times \mathcal E^\ast \rightarrow \mathcal X, where \mathcal E^\ast stands for the set of all possible sequences of events.

Language generated by the automaton is \mathcal L(\mathcal G) = \{s\in\mathcal E^\ast \mid f(x_0,s) \;\text{is defined}\}

Language marked by the automaton (the automaton is accepting or recognizing that language) \mathcal L_\mathrm{m}(\mathcal G) = \{s\in\mathcal L(\mathcal G) \mid f(x_0,s) \in \mathcal{X}_\mathrm{m}\}

Example 14 (Language accepted by automaton) \mathcal{E} = \{a,b\}, \mathcal{L} = \{a,aa,ba,aaa,aba,baa,bba,\ldots\}

G init init 0 0 init->0 1 1 1->1 a 1->0 b 0->1 a 0->0 b
Figure 15: Example of an automaton generating the language \mathcal{L} = \{a,aa,ba,aaa,aba,baa,bba,\ldots\}

What if we remove the self loop at state 0? The automaton then accepts languages starting with a and with b being the last event or immediately followed by a.

What is the language view of automata good for?

  • Definitions, analysis, synthesis.
  • We then need language concepts such as
    • concatenation of strings: \quad c = ab
    • empty string \varepsilon: \quad\varepsilon a = a \varepsilon = a
    • prefix, suffix
    • prefix closure \bar{\mathcal{L}} (of the language \mathcal L)
    • …

Blocking

An important concept in automata is blocking. A state is blocking if there is no transition out of it. An example follows.

Example 15 (Blocking states) In the automaton in Fig 16, state 2 is blocking. It is a deadlock state. States 3 and 4 are livelock states.

G init init 0 0 init->0 2 2 2->0 g 1 1 0->1 a 1->2 b 5 5 1->5 g 3 3 1->3 a 4 4 3->4 b 4->3 a 4->4 g
Figure 16: Example of an automaton with blocking states

Language characterization: \bar{\mathcal{L}}_\mathrm{m}(\mathcal G) \sub \mathcal L(\mathcal G).

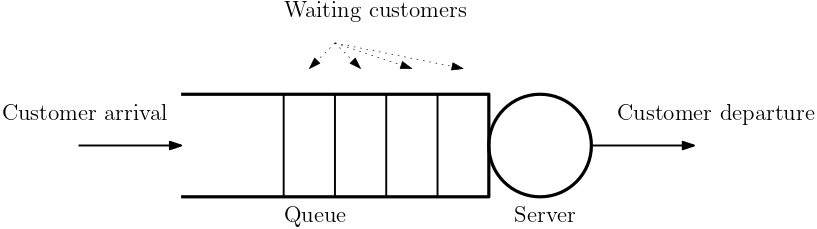
Queueing systems

Queueing systems are a particular and very useful class of discrete-event systems. They consist of these three components:

  • entities (also customers, jobs, tasks, requests, etc.)
  • resources (also servers, processors, etc.): customers are waiting for them
  • queues (also buffers): where waiting is done

A common graphical representation that contains all these three compoments is in Fig 17.

Figure 17: Queueing system

Examples of queueing systems

  • entities: people waiting for service in a bank or at a bust stop
  • resources: people (again) in a bank at the counter
  • queues: bank lobbies, bus stops, warehouses, …
Note

What are other examples?

  • entities: packets, …
  • resources: processor, computer periphery, router, …
  • queues: …

Why shall we study queueing systems?

  • Resources are not unlimited
  • Tradeoff needed between customer satisfaction and fair resources allocation

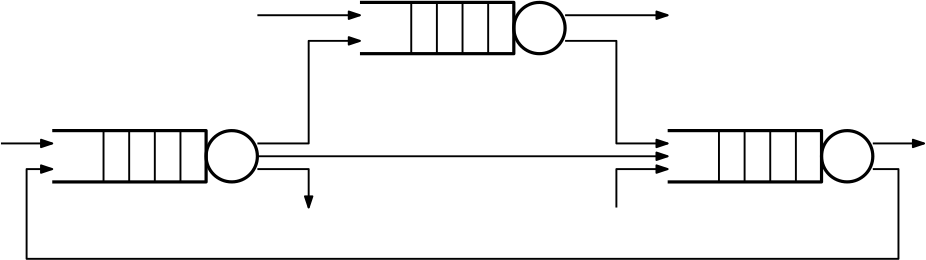
Networks of queueing systems

Queueing systems can be interconnected into networks.

Figure 18: Example of a network of queueing systems

Queueing systems as automata

The reason why we mentioned queueing systems in this part of our course is that they can be modelled as automata. And we already know that in order to define and automaton, we must characterize the key components defining the automaton – three in this case:

  • events: \mathcal E = \{\text{arrival},\text{departure}\};

  • states: number of customers in the queue \mathcal X = \{0,1,2,3,\ldots\}, \quad \mathcal X_0 = \{0\},

Note

Obviously this is not a finite state automation – unless the queue is bounded – and whether the queue’s length is bounded is a modelling assumption.

  • state transition: f(x,e) = \begin{cases} x+1, & \text{if}\; x\leq 0 \land e = \mathrm{arrival}\\ x-1, & \text{if}\; x > 0 \land e = \mathrm{departure}. \end{cases}

Queueing system as an automaton

Figure 19: Queueing system as an automaton
Note

Note how the states correspond to the value of the state variable.

Example 16 (Example of a queueing system: jobs processing by a CPU) …

Stochastic queueing systems

An important extension of the basic concept of a queueing system is the introduction of randomness. In particular, the arrivals can be modelled using random processes. Similarly, the departures given by the delays (the processing time) of the server can be modelled as random.

Obviously, the time needs to be included in the automaton, and so far we do not have it there. It is then high time to introduce it.

Timed automaton

So far, even if the automaton corresponded to a physical system (and did not just represent a generator of a language), the time was not included. The transitions were triggered by the events, but we did not specify the time at which the event occurred.

There are, however, many situations when it is useful or even crucial to incorporate time. We can then answer questions such as

  • How many events of a certain type in a given interval?
  • Is the time interval between two events above a given threshold?
  • How long does the system spend in a given state?
  • …

There are several ways how to incorporate time into the automaton. We will follow the concept of a timed automaton with guards (introduced by Alur and Dill). Within their framework we have

  • one or several resettable clocks: c_i,\, i=1,\ldots, k, driven by the ODE \frac{\mathrm{d} c_i(t)}{\mathrm d t} = 1, \quad c_i(0) = 0;
  • each transition labelled by the tripple {guard; event; reset}.
Note

Both satisfaction of the guard and arrival of the event constitute enabling conditions for the transition. They could be wrapped into a single compound condition.

Example 17 (Timed automaton with guards)  

G init init 0 0 init->0 1 1 0->1 -; msg; c₁ 1->1 c₁≥1; msg; c₁ 2 2 1->2 0<c₁<1; msg; c₁ 3 3 2->3 c₁<1; alarm; -
Figure 20: Example of a timed automaton with guards

Example 18 (Timed automaton with guards and invariant)  

G init init 0 0 init->0 2 2 c₁<1 3 3 2->3 -; alarm; - 1 1 0->1 -; msg; c₁ 1->2 0<c₁<1; msg; c₁ 1->1 c₁≥1; msg; c₁
Figure 21: Example of a timed automaton with guards and invariant

Invariant vs guard

  • Invariant (of a location) gives an upper bound on the time the system can stay at the given location. It can leave earlier but not later.
  • Guard (of a given transition) gives an enabling condition on leaving the location through the given transition.

Example 19 (Several trains approaching a bridge) The example is taken from [1] and is included in the demos coming with the Uppaal tool.

Back to top

References

[1]
G. Behrmann, A. David, and K. G. Larsen, “A Tutorial on Uppaal,” in Formal Methods for the Design of Real-Time Systems, M. Bernardo and F. Corradini, Eds., in Lecture Notes in Computer Science, no. 3185., Berlin, Heidelberg: Springer, 2004, pp. 200–236. doi: 10.1007/978-3-540-30080-9_7.